题目内容
过抛物线y2=4x的焦点作直线AB交抛物线于A、B,若AB中点M(2,1)求直线AB方程.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题知直线AB的斜率存在设斜率为且k≠0,根据
=4x1,
=4x2,可得k=
=
的值,点斜式求得AB所在直线的方程.
| y | 2 1 |
| y | 2 2 |
| y1-y2 |
| x1-x2 |
| 4 |
| y1+y2 |
解答:
解:设A(x1,y1),B(x2,y2),则y12=4x1,y22=4x2
∴(y1+y2)(y1-y2)=4(x1-x2),∴(y1+y2)•k=4
∵y1+y2=2y=2,∴k=2
∴直线AB方程为y=2x-3.
∴(y1+y2)(y1-y2)=4(x1-x2),∴(y1+y2)•k=4
∵y1+y2=2y=2,∴k=2
∴直线AB方程为y=2x-3.
点评:本题考查直线和圆锥曲线的位置关系及中点弦问题,利用点差法求出直线的斜率,是解题的关键,属于基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
若实数x,y满足约束条件
,则z=x+y的最大值是4,则a=( )
|
| A、2 | B、3 | C、3或1 | D、4 |
已知函数f(x)=
对任意x1,x2∈R(x1≠x2),恒有(x1-x2)[f(x1)-f(x2)]>0
,则实数a的取值范围为( )
|
,则实数a的取值范围为( )
| A、(1,+∞) |
| B、[4,8) |
| C、(4,8) |
| D、(1,8) |
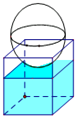 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为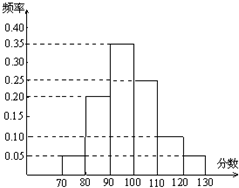 某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.