题目内容
下列关于命题的说法错误的是( )
A.命题“若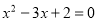 ,则
,则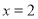 ” 的逆否命题是“若
” 的逆否命题是“若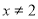 ,则
,则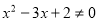 ”
”
B.“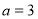 ”是“函数
”是“函数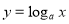 在其定义域上为增函数”的充分不必要条件
在其定义域上为增函数”的充分不必要条件
C.若命题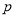 :
: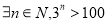 ,则
,则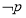 :
: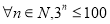
D.命题“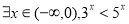 ”是真命题
”是真命题
练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
题目内容
下列关于命题的说法错误的是( )
A.命题“若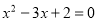 ,则
,则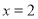 ” 的逆否命题是“若
” 的逆否命题是“若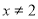 ,则
,则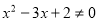 ”
”
B.“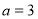 ”是“函数
”是“函数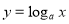 在其定义域上为增函数”的充分不必要条件
在其定义域上为增函数”的充分不必要条件
C.若命题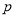 :
: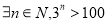 ,则
,则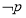 :
: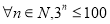
D.命题“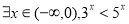 ”是真命题
”是真命题
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案