题目内容
已知数列{an}，{bn}，满足a1=b1=3，an+1-an=
=3，n∈N*，若数列{cn}满足cn=b an，则c2013=（ ）
| bn+1 |
| bn |
| A、92012 |
| B、272012 |
| C、92013 |
| D、272013 |
考点：数列递推式
专题：新定义,等差数列与等比数列
分析：本题可先等差数列{an}和等比数列{bn}的通项，再利用数列{cn}的通项公式得到所求结论．
解答：
解：∵数列{an}，满足a1=3，an+1-an=3，n∈N*，
∴an=a1+（n-1）d=3+3（n-1）=3n．
∵数列{bn}，满足b1=3，
=3，n∈N*，
∴bn=b1•qn-1=3×3n-1=3n．
∵数列{cn}满足cn=b an，
∴c2013=ba2013=b6039=36039=272013．
故选D．
∴an=a1+（n-1）d=3+3（n-1）=3n．
∵数列{bn}，满足b1=3，
| bn+1 |
| bn |
∴bn=b1•qn-1=3×3n-1=3n．
∵数列{cn}满足cn=b an，
∴c2013=ba2013=b6039=36039=272013．
故选D．
点评：本题先利用等差数列和等比数列的通项公式求出数列的通项，再用通项公式求出新数列中的项，本题思维量不大，属于基础题．
练习册系列答案
相关题目
假设一直角三角形的两直角边的长都是区间（0，1）内的随机数，则斜边长小于
的概率为（ ）
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若函数f（x）=2sin（2x+
），则它的图象的一个对称中心为（ ）
| π |
| 4 |
A、（-
| ||
B、（
| ||
| C、（0，0） | ||
D、（-
|
若θ为三角形一个内角，且对任意实数x，y=x2cosθ-4xsinθ+6均取正值，则cosθ所在区间为（ ）
A、（
| ||
B、（0，
| ||
C、（-2，
| ||
D、（-1，
|
若方程
+
=1表示准线平行于x轴的椭圆，则m的范围是（ ）
| x2 |
| m2 |
| y2 |
| (1-m)2 |
A、m＞
| ||
B、m＜
| ||
C、m＞
| ||
D、m＜
|
在等比数列{an}中，如果a6=6，a9=9，那么a3为（ ）
| A、4 | ||
B、
| ||
C、
| ||
| D、2 |
“a=2”是“直线2x+ay+2=0与直线ax+2y-2=0平行”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数f（x）=
为R的单调函数，则实数a的取值范围是（ ）
|
| A、（0，+∞） |
| B、[-1，0） |
| C、（-2，0） |
| D、（-∞，-2） |
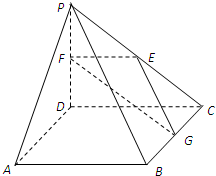如图，在四棱锥P-ABCD中，ABCD是正方形，PD⊥平面ABCD，PD=AB=2，E，F，G分别是PC，PD，BC的中点．