题目内容
已知f(x)=(
)2-x2,g(x)=(
)3x,当f(x)>g(x)时,求x的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
考点:指、对数不等式的解法
专题:函数的性质及应用
分析:根据指数函数的单调性即可解不等式.
解答:
解:由f(x)>g(x)得(
)2-x2>(
)3x,
即2-x2<3x,
则x2+3x-2>0,
解得x>
或x<
,
故x的取值范围是{x|x>
或x<
}.
| 1 |
| 2 |
| 1 |
| 2 |
即2-x2<3x,
则x2+3x-2>0,
解得x>
-3+
| ||
| 2 |
-3-
| ||
| 2 |
故x的取值范围是{x|x>
-3+
| ||
| 2 |
-3-
| ||
| 2 |
点评:本题主要考查不等式的求解,根据指数函数的单调性是解决本题的关键.

练习册系列答案
相关题目
已知直线a,b,平面α,β,且a⊥α,b?β,则“a⊥b”是“α∥β”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知函数f(x)对于任意的x∈R都有f(x)<f(x+1),则f(x)在R上( )
| A、是单调增函数 |
| B、没有单调减区间 |
| C、可能存在单调增区间,也可能不存在单调增区间 |
| D、没有单调增区间 |
如果|
|=|
|=1,
与
的夹角为θ,
•
=
,则θ=( )
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| A、90° | B、30° |
| C、60° | D、120° |
设集合M={x|x=
,k∈Z},N={x|x=
+
,k∈Z},则M、N之间的关系为( )
| kπ |
| 2 |
| + |
. |
| π |
| 4 |
| kπ |
| 4 |
| π |
| 2 |
| A、M?N | B、M?N |
| C、M=N | D、M∩N=∅ |
如图为函数f(x)=t+logax的图象(a,t均为实常数),则下列结论正确的是 ( )
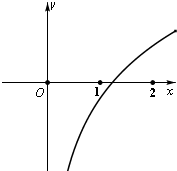

| A、0<a<1,t<0 |
| B、0<a<1,t>0 |
| C、a>1,t<0 |
| D、a>1,t>0 |