题目内容
 如图,在正三棱柱ABC-A1B1C1中,AB=1,AA1=2,M是AB1上的动点,且AM=λAB1,N是CC1的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=1,AA1=2,M是AB1上的动点,且AM=λAB1,N是CC1的中点.(Ⅰ)若λ=
| 1 |
| 2 |
(Ⅱ)若直线MN与平面ABN所成角的正弦值为
|
考点:直线与平面所成的角
专题:综合题,空间位置关系与距离
分析:(Ⅰ)取AB中点E,连结ME,CE,证明MN∥CE,利用AA1⊥面ABC,即可证明MN⊥AA1;
(Ⅱ)以AB,AA1为x轴,z轴,在面ABC内以过A点且垂直于AB的射线为y轴建系,求出平面ABN的法向量,利用直线MN与平面ABN所成角的正弦值为
,即可求λ的值.
(Ⅱ)以AB,AA1为x轴,z轴,在面ABC内以过A点且垂直于AB的射线为y轴建系,求出平面ABN的法向量,利用直线MN与平面ABN所成角的正弦值为
|
解答:
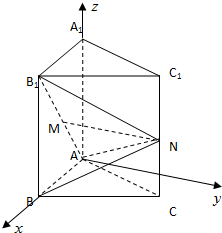 (Ⅰ)证明:取AB中点E,连结ME,CE,则有ME与NC平行且相等.
(Ⅰ)证明:取AB中点E,连结ME,CE,则有ME与NC平行且相等.
∴四边形MNCE为平行四边形,MN∥CE …(2分)
∵AA1⊥面ABC,CE?面ABC,
∴AA1⊥CE,∴MN⊥AA1.…(4分)
(Ⅱ)解:以AB,AA1为x轴,z轴,在面ABC内以过A点且垂直于AB的射线为y轴建系如图,B(1,0,0),N(
,
,1),B1(1,0,2),M(λ,0,2λ),
=(
-λ,
,1-2λ),
=(1,0,0),
=(
,
,1)
…(6分)
设
=(x,y,z)是平面ABN的一个法向量,则
∴
∴
,令y=1,∴
=(0,1,-
)…(8分)
设MN与面ABN所成角为θ,
则sinθ=|cos<
,
>|=
=
…(10分)
=
,化简得3λ2+5λ-2=0,λ=-2或λ=
,
由题意知λ>0,∴λ=
.…(12分)
 (Ⅰ)证明:取AB中点E,连结ME,CE,则有ME与NC平行且相等.
(Ⅰ)证明:取AB中点E,连结ME,CE,则有ME与NC平行且相等.∴四边形MNCE为平行四边形,MN∥CE …(2分)
∵AA1⊥面ABC,CE?面ABC,
∴AA1⊥CE,∴MN⊥AA1.…(4分)
(Ⅱ)解:以AB,AA1为x轴,z轴,在面ABC内以过A点且垂直于AB的射线为y轴建系如图,B(1,0,0),N(
| 1 |
| 2 |
| ||
| 2 |
| MN |
| 1 |
| 2 |
| ||
| 2 |
| AB |
| AN |
| 1 |
| 2 |
| ||
| 2 |
…(6分)
设
| n1 |
|
∴
|
|
| n1 |
| ||
| 2 |
设MN与面ABN所成角为θ,
则sinθ=|cos<
| MN |
| n1 |
| ||||||||||
|
|
| λ | ||||||
|
| 1 | ||
|
| 1 |
| 3 |
由题意知λ>0,∴λ=
| 1 |
| 3 |
点评:本题考查线面垂直的性质,考查线面角,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 如图,多面体ABCC1A1B1中,四边形AA1C1C是正方形,四边形BCC1B1是直角梯形,CC1⊥BC且BC∥B1C1.△ACB、△A1C1B1都是等腰直角三角形,A、B1分别为直角顶点,M是B1B上的点,BM=2MB1.
如图,多面体ABCC1A1B1中,四边形AA1C1C是正方形,四边形BCC1B1是直角梯形,CC1⊥BC且BC∥B1C1.△ACB、△A1C1B1都是等腰直角三角形,A、B1分别为直角顶点,M是B1B上的点,BM=2MB1. 太阳岛公园引进了两种植物品种甲与乙,株数分别为18与12,这30株植物的株高编写成茎叶图如图(单位:cm):若这两种植物株高在185cm以上(包括185cm)定义为“优秀品种”,株高在185cm以下(不包括185cm)定义为“非优秀品种”.
太阳岛公园引进了两种植物品种甲与乙,株数分别为18与12,这30株植物的株高编写成茎叶图如图(单位:cm):若这两种植物株高在185cm以上(包括185cm)定义为“优秀品种”,株高在185cm以下(不包括185cm)定义为“非优秀品种”.