题目内容
10.若不等式组$\left\{\begin{array}{l}{x+y-3≥0}\\{y≤kx+3}\\{0≤x≤2}\end{array}\right.$表示的平面区域是一个锐角三角形,则实数k的取值范围是( )| A. | (-∞,-1) | B. | (-1,0) | C. | (1,+∞) | D. | (0,1) |
分析 作出平面区域,易得边界点的坐标,考虑特殊位置数形结合可得.
解答 解:作出不等式组$\left\{\begin{array}{l}{x+y-3≥0}\\{y≤kx+3}\\{0≤x≤2}\end{array}\right.$表示的平面区域(如图阴影)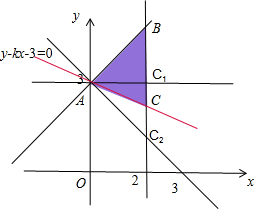
易得边界点A(0,3),B(2,5),C(2,2k+3)
当C点与C1(2,35)重合或与C2(2,1)重合时,△ABC是直角三角形,
当点C位于B、C1之间,或在C1C2的延长线上时,△ABC是钝角三角形,
当点C位于C1、C2之间时,△ABC是锐角三角形,点C在其它的位置不能构成三角形
综上所述,可得1<2k+3<3,解得-1<k<0
故选:B.
点评 本题考查简单线性规划,涉及三角形的形状,数形结合分类讨论是解决问题的关键,属中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
19.已知全集U=R,集合A={x|x<1},则∁UA=( )
| A. | (-∞,1] | B. | [1,+∞) | C. | R | D. | (1,+∞) |
5.已知全集U=R,集合A={x|x(x-1)≥0},则∁UA=( )
| A. | [0,1] | B. | [1,+∞) | C. | (0,1) | D. | (-∞,0)∪(1,+∞) |
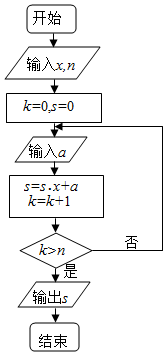 秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为( )
秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为( ) ,那么 ( )
,那么 ( ) B.
B. C.
C. D.
D.
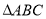 中,内角
中,内角 ,
,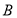 ,
, 所对的边分别为
所对的边分别为 ,
, ,
,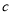 ,已知
,已知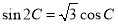 ,其中
,其中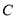 为锐角.
为锐角. 的大小;
的大小;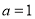 ,
, ,求边
,求边 的长.
的长. 表示的平面区域(阴影部分)是( )
表示的平面区域(阴影部分)是( )
 ,则
,则 ( )
( )