题目内容
5.已知f(n)=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$,且g(n)=$\frac{1}{f(n)-1}$[f(1)+f(2)+…十f(n-1)].(1)写出g(2),g(3),g(4)的值;
(2)归纳g(n)的值,并用数学归纳法加以证明.
分析 (1)f(1)=1,f(2)=$\frac{3}{2}$,f(3)=$\frac{11}{6}$,f(4)=$\frac{25}{12}$.可得g(2)=$\frac{1}{f(2)-1}$×f(1)=2,g(3)=3,g(4)=4.
(2)由(1)猜想g(n)=n(n≥2).利用数学归纳法证明即可.
解答 解:(1)f(1)=1,f(2)=1+$\frac{1}{2}$=$\frac{3}{2}$,f(3)=1+$\frac{1}{2}$+$\frac{1}{3}$=$\frac{11}{6}$,f(4)=1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$=$\frac{25}{12}$.
∴g(2)=$\frac{1}{f(2)-1}$×f(1)=2,g(3)=$\frac{1}{f(3)-1}$[f(1)+f(2)]=3,g(4)=$\frac{1}{f(4)-1}$[f(1)+f(2)+f(3)]=4.
(2)由(1)猜想g(n)=n(n≥2).
下面利用数学归纳法证明:
①当n=2时成立;
②假设当n=k(k∈N*,k≥2)时,g(k)=k.
即g(k)=$\frac{1}{f(k)-1}$[f(1)+f(2)+…+f(k-1)]=k,
∴f(1)+f(2)+…+f(k-1)=kf(k)-k,
则当n=k+1时,g(k+1)=$\frac{1}{f(k+1)-1}$[f(1)+f(2)+…+f(k)]
=$\frac{1}{f(k)+\frac{1}{k+1}-1}$•[(k+1)f(k)-k]
=k+1.
因此当n=k+1时,命题g(k+1)=k+1成立.
综上可得:?n∈N*,g(n)=n(n≥2)成立.
点评 本题考查了递推关系、数学归纳法,考查了猜想能力、推理能力与计算能力,属于中档题.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案 从甲、乙两种玉米中各抽测了10株玉米苗的高度(单位:cm),其茎叶图如图所示,根据茎叶图,下列描述正确的是( )
从甲、乙两种玉米中各抽测了10株玉米苗的高度(单位:cm),其茎叶图如图所示,根据茎叶图,下列描述正确的是( )| A. | 甲种玉米苗的平均高度大于乙种玉米苗的高度,且甲种玉米苗比乙种玉米苗长得整齐 | |
| B. | 甲种玉米苗的平均高度大于乙种玉米苗的高度,但乙种玉米苗比甲种玉米苗长得整齐 | |
| C. | 乙种玉米苗的平均高度大于甲种玉米苗的高度,且乙种玉米苗比甲种玉米苗长得整齐 | |
| D. | 乙种玉米苗的平均高度大于甲种玉米苗的高度,但甲种玉米苗比乙种玉米苗长得整齐 |
| A. | $\left\{{x\left|{x<\frac{1}{2}}\right.}\right\}$ | B. | $\left\{{x\left|{x>\frac{1}{2}}\right.}\right\}$ | C. | {x|x≥-1} | D. | {x|x<3} |
| A. | $\sqrt{5-2\sqrt{3}}$ | B. | $\sqrt{5-2\sqrt{2}}$ | C. | $\sqrt{4-2\sqrt{2}}$ | D. | $\sqrt{3-\sqrt{3}}$ |
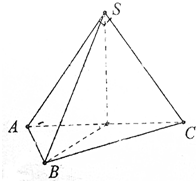 在三棱锥S-ABC中,∠ASB=∠BSC=60°,∠ASC=90°,且SA=SB=SC,求证:平面ASC⊥平面ABC.
在三棱锥S-ABC中,∠ASB=∠BSC=60°,∠ASC=90°,且SA=SB=SC,求证:平面ASC⊥平面ABC.