题目内容
14.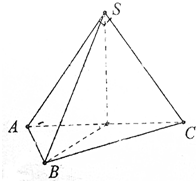 在三棱锥S-ABC中,∠ASB=∠BSC=60°,∠ASC=90°,且SA=SB=SC,求证:平面ASC⊥平面ABC.
在三棱锥S-ABC中,∠ASB=∠BSC=60°,∠ASC=90°,且SA=SB=SC,求证:平面ASC⊥平面ABC.
分析 令SA=SB=SC=a,结合条件,求得AB=BC=a,AC=$\sqrt{2}$a,有勾股定理的逆定理,可得△ABC为直角三角形,取AB的中点O,连接SO,BO,由线面垂直的判定定理,可得SO⊥平面ABC,再由面面垂直的判定定理,即可得证.
解答  证明:令SA=SB=SC=a,
证明:令SA=SB=SC=a,
由∠ASB=∠BSC=60°,∠ASC=90°,
即有AB=BC=a,AC=$\sqrt{2}$a,
则△ABC为直角三角形,且∠ABC=90°,
取AB的中点O,连接SO,BO,
由SA=SB,可得SO⊥AC,
由SB=a,OB=SO=$\frac{\sqrt{2}}{2}$a,即有SO⊥OB,
由OB∩AC=O,
可得SO⊥平面ABC,
由SO?平面SAC,
则平面SAC⊥平面ABC.
点评 本题考查面面垂直的判定定理的运用,考查空间线面的位置关系,属于中档题.

练习册系列答案
相关题目
6.设x>0,函数f(x)=x•3x-318的零点,x0∈(k,k+1)(k∈N*),则k=( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
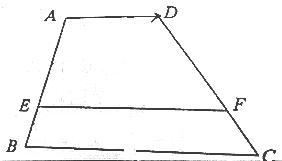 如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.
如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.