题目内容
2.已知函数f(x)=|2x+a|+|2x-2b|+3(Ⅰ)若a=1,b=1,求不等式f(x)>8的解集;
(Ⅱ)当a>0,b>0时,若f(x)的最小值为5,求$\frac{1}{a}$+$\frac{1}{b}$的最小值.
分析 (Ⅰ)若a=1,b=1,不等式f(x)>8为|2x+1|+|2x-2|>5,分类讨论求不等式f(x)>8的解集;
(Ⅱ)f(x)的最小值为a+2b+3,利用“1”的代换,结合基本不等式,即可得出结论.
解答 解:(Ⅰ)若a=1,b=1,不等式f(x)>8为|2x+1|+|2x-2|>5
x≥1,不等式可化为4x-1>5,∴x>1.5,
-0.5<x<1,不等式可化为3>5,不成立,
x≤-0.5,不等式可化为1-4x>5,∴x<-1,
综上所述,不等式的解集为{x|x<-1或x>1.5};
(Ⅱ)f(x)=|2x+a|+|2x-2b|+3≥|2x+a-2x+2b|+3=|a+2b|+3,
∵a>0,b>0,∴f(x)的最小值为a+2b+3,
∴a+2b+3=5,∴a+2b=2,
∴$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{2}$($\frac{1}{a}$+$\frac{1}{b}$)(a+2b)=$\frac{1}{2}$(3+$\frac{2b}{a}$+$\frac{a}{b}$)≥$\frac{3+2\sqrt{2}}{2}$,
∴$\frac{1}{a}$+$\frac{1}{b}$的最小值为$\frac{3+2\sqrt{2}}{2}$.
点评 本题考查不等式的解法,考查绝对值不等式的运用,考查基本不等式,属于中档题.

练习册系列答案
相关题目
12.某公司在销售某种环保材料过程中,记录了每日的销售量x(吨)与利润y(万元)的对应数据,下表是其中的几组对应数据,由此表中的数据得到了y关于x的线性回归方程$\widehat{y}$=0.7x+a,若每日销售量达到10吨,则每日利润大约是( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | 7.2万元 | B. | 7.35万元 | C. | 7.45万元 | D. | 7.5万元 |
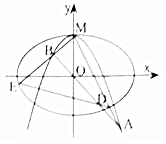 如图,抛物线C1:y=b-x2经过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点及上顶点M,过点M的两条互相垂直的直线l1,l2分别交抛物线于A,B两点,交椭圆于D,E两点,已知抛物线C1:y=b-x2与x轴所围成的区域面积为$\frac{4}{3}$.
如图,抛物线C1:y=b-x2经过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点及上顶点M,过点M的两条互相垂直的直线l1,l2分别交抛物线于A,B两点,交椭圆于D,E两点,已知抛物线C1:y=b-x2与x轴所围成的区域面积为$\frac{4}{3}$.