题目内容
6.已知函数f(x)=|x-a|-$\frac{9}{x}$,x∈[1,6].(1)a=1,解不等式f(x)≤1;
(2)x∈[1,6],f(x)≤5恒成立,求实数a的取值范围.
分析 (1)当a=1时,函数f(x)=x-1-$\frac{9}{x}$,在[1,6]上为增函数,求得f(x)=1时x的值,可得不等式式f(x)≤1的解集.
(2)x∈[1,6]时,f(x)≤5恒成立,故f(x)max≤5.根据函数f(x)=|x-a|-$\frac{9}{x}$,分类讨论求得f(x)max,可得a的范围.
解答 解:(1)当a=1时,函数f(x)=|x-1|-$\frac{9}{x}$=x-1-$\frac{9}{x}$,在[1,6]上为增函数,
不等式f(x)≤1,即 x-1-$\frac{9}{x}$≤1,
由x-1-$\frac{9}{x}$=1求得x=1+$\sqrt{10}$,故不等式的解集为[1,1+$\sqrt{10}$].
(2)∵x∈[1,6]时,f(x)≤5恒成立,故f(x)max≤5.
由于函数f(x)=|x-a|-$\frac{9}{x}$,
①当a≤1时,f(x)=x-a-$\frac{9}{x}$,
f(x)在[1,6]上为增函数,故f(x)max=f(6)=$\frac{9-a}{2}$≤5,求得a≥-1,故此时,-1≤a≤1.
②当1<a<3时,f(x)=$\left\{\begin{array}{l}{a-x-\frac{9}{x},1≤x<a}\\{x-a-\frac{9}{x},a≤x≤6}\end{array}\right.$,
∴当1≤x<a<3时,f′(x)=-1+$\frac{9}{{x}^{2}}$>0,∴f(x)是增函数;
当a≤x≤6时,f′(x)=1+$\frac{9}{{x}^{2}}$>0,∴f(x)是增函数;
故f(x)在在[1,6]上递增,故f(x)max=f(6)=6-a-$\frac{9}{6}$≤5,求得 a≥-$\frac{1}{2}$,故此时,1<a<3.
③当3≤a≤6时,f(x)=$\left\{\begin{array}{l}{a-x-\frac{9}{x},1≤x<a}\\{x-a-\frac{9}{x},a≤x≤6}\end{array}\right.$,
当1≤x<a时,f′(x)=-1+$\frac{9}{{x}^{2}}$<0,∴f(x)是减函数,
当a≤x≤6时,f′(x)=1+$\frac{9}{{x}^{2}}$>0,∴f(x)是增函数,
再根据f(1)=a-1-9=a-10,f(6)=6-a-$\frac{9}{x}$,∴f(x)max=f(6)=6-a-$\frac{9}{6}$≤5,求得 a≥-$\frac{1}{2}$,故此时,3≤a≤6.
④当a>6时,f(x)=|x-a|-$\frac{9}{x}$=a-x-$\frac{9}{x}$=a-(x+$\frac{9}{x}$)≤a-6,
故f(x)max=a-6,由a-6≤5,求得a≤11,故此时,6<a≤11.
综合①②③④,可得a的范围为[-1,11].
点评 本题主要考查绝对值不等式的解法,分段函数的应用,函数的恒成立问题,利用导数研究函数的最大值,属于难题.

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
| A. | 第一象限的角 | B. | 第二象限的角 | C. | 第三象限的角 | D. | 第四象限的角 |
| A. | 在x轴上 | B. | 在y轴上 | C. | 当a>b时,在x轴上 | D. | 当a>b时,在y轴上 |
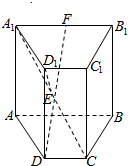 已知四棱柱ABCD-A1B1C1D1的侧棱AA1⊥底面ABCD,ABCD是等腰梯形,AB∥DC,AB=2,AD=1,∠ABC=60°,E,F分别是A1C,A1B1的中点.
已知四棱柱ABCD-A1B1C1D1的侧棱AA1⊥底面ABCD,ABCD是等腰梯形,AB∥DC,AB=2,AD=1,∠ABC=60°,E,F分别是A1C,A1B1的中点.