题目内容
下面说法正确的是( )
| A、命题“?x∈R,使得x2+x+1≥0”的否定是“?x∈R,使得x2+x+1≥0” |
| B、实数x>y是x2>y2成立的充要条件 |
| C、设p,q为简单命题,若“p∨q”为假命题,则“?p∧?q”也为假命题 |
| D、命题“α=0,则cosα=1”的逆否命题为真命题 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:通过特称命题的否定判断A的正误;充要条件判断B的正误;复合命题的真假判断C的正误;逆否命题的真假判断D的正误;
解答:
解:对于A,命题“?x∈R,使得x2+x+1≥0”的否定是“?x∈R,使得x2+x+1≥0”,不满足特称命题的否定形式,所以A不正确.
对于B,实数x>y是x2>y2成立的充要条件,因为|x|>|y|是x2>y2成立的充要条件,所以B不正确;
对于C,设p,q为简单命题,若“p∨q”为假命题,可能两个命题都是假命题,则“?p∧?q”也为真命题,
所以C不正确.
对于D,命题“α=0,则cosα=1”的逆否命题为真命题,因为原命题是真命题,所以D正确.
故选:D.
对于B,实数x>y是x2>y2成立的充要条件,因为|x|>|y|是x2>y2成立的充要条件,所以B不正确;
对于C,设p,q为简单命题,若“p∨q”为假命题,可能两个命题都是假命题,则“?p∧?q”也为真命题,
所以C不正确.
对于D,命题“α=0,则cosα=1”的逆否命题为真命题,因为原命题是真命题,所以D正确.
故选:D.
点评:本题考查命题的真假的判断,充要条件以及命题的否定四种命题的逆否关系,基本知识的考查.

练习册系列答案
相关题目
下列选项中,p是q的必要不充分条件的是( )
| A、p:a+c>b+dq:a>b且c>d | ||
| B、p:x=1q:x=x2 | ||
| C、p:a+bi(a,b∈R)是纯虚数q:a=0 | ||
D、p:f(x)=x3+2x2+mx+1在R上单调递增q:m≥
|
两条异面直线指的是( )
| A、不同在某个平面内的两条直线 |
| B、分别在某两个平面内的两条直线 |
| C、既不平行又不相交的两条直线 |
| D、平面内的一条直线和平面外的一条直线 |
阅读如图的程序框图,运行相应的程序,则输出i的值为( )


| A、3 | B、4 | C、5 | D、6 |
已知函数f(x)=x3+x,a、b∈R,且a+b>0,则f(a)+f(b)的值一定( )
| A、大于零 | B、小于零 |
| C、等于零 | D、正负都有可能 |
若满足条件AB=
,C=
的三角形有两个,则边长BC的取值范围是( )
| 3 |
| π |
| 3 |
| A、(1,2) | ||||
B、(
| ||||
C、(
| ||||
D、(
|
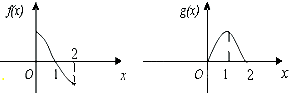 已知偶函数f(x)与奇函数g(x)的定义域都是(-2,2),它们在[0,2]上的图象如图所示,则使关于x的不等式f(x)•g(x)>0成立的x的取值范围为( )
已知偶函数f(x)与奇函数g(x)的定义域都是(-2,2),它们在[0,2]上的图象如图所示,则使关于x的不等式f(x)•g(x)>0成立的x的取值范围为( )| A、(-2,-1)∪(1,2) |
| B、(-1,0)∪(0,1) |
| C、(-2,-1)∪(0,1) |
| D、(-1,0)∪(1,2) |
数列{an}中,已知a1=1,an+1=
,则an为( )
| an |
| 2an+1 |
| A、2n-1 | ||
| B、2n+1 | ||
C、
| ||
D、
|