题目内容
直线x-y-1=0与圆（x-1）2+（y-2）2=4相交于A、B两点，则弦AB的长为（ ）
A、
| ||
B、2
| ||
C、
| ||
D、2
|
考点：直线与圆的位置关系
专题：计算题,直线与圆
分析：利用点到直线的距离公式可得：圆心到直线x-y-1=0的距离d，即可得出弦长|AB|．
解答：
解：由圆（x-1）2+（y-2）2=4，可得圆心M（1，2），半径r=2．
∴圆心到直线x-y-1=0的距离d=
=
．
∴弦长|AB|=2
=2
．
故选：B．
∴圆心到直线x-y-1=0的距离d=
| 2 | ||
|
| 2 |
∴弦长|AB|=2
| 4-2 |
| 2 |
故选：B．
点评：本题考查了直线与圆的位置关系、点到直线的距离公式，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知x＞1，则函数f（x）=x+1+
的最小值为（ ）
| 1 |
| x-1 |
| A、1 | B、2 | C、3 | D、4 |
下列四个函数中，在（0，+∞）上为增函数的是（ ）
| A、f（x）=3-x | ||
| B、f（x）=x2-3 | ||
C、f（x）=
| ||
| D、f（x）=-x2 |
两条异面直线指的是（ ）
| A、不同在某个平面内的两条直线 |
| B、分别在某两个平面内的两条直线 |
| C、既不平行又不相交的两条直线 |
| D、平面内的一条直线和平面外的一条直线 |
S是△ABC所在平面外一点，SA=SB=SC，则S在平面ABC内的射影O是△ABC的（ ）
| A、内心 | B、外心 | C、重心 | D、垂心 |
阅读如图的程序框图，运行相应的程序，则输出i的值为（ ）
| A、3 | B、4 | C、5 | D、6 |
已知函数f（x）=x3+x，a、b∈R，且a+b＞0，则f（a）+f（b）的值一定（ ）
| A、大于零 | B、小于零 |
| C、等于零 | D、正负都有可能 |
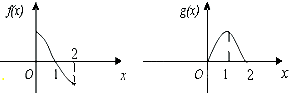已知偶函数f（x）与奇函数g（x）的定义域都是（-2，2），它们在[0，2]上的图象如图所示，则使关于x的不等式f（x）•g（x）＞0成立的x的取值范围为（ ）| A、（-2，-1）∪（1，2） |
| B、（-1，0）∪（0，1） |
| C、（-2，-1）∪（0，1） |
| D、（-1，0）∪（1，2） |
已知平面向量
，
，
满足|
|=1，|
|=2，|
|=3，且
，
，
两两所成的角相等，则|
+
+
|等于（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
A、
| ||
| B、6 | ||
C、6或
| ||
D、6或
|