题目内容
6.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点到其渐近线的距离等于实轴长,且P(2,2)为双曲线上的点,则该双曲线的方程为( )| A. | x2-$\frac{3{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{12}$=1 | C. | x2-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{3}$=1 |
分析 求出双曲线的焦点和渐近线方程,由点到直线的距离公式可得b=2a,将P的坐标代入双曲线方程,解方程组可得a,b,进而得到所求双曲线的方程.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点(c,0)到其渐近线y=$\frac{b}{a}$x的距离
为d=$\frac{|bc|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{bc}{c}$=b,
由题意可得b=2a,①
P(2,2)为双曲线上的点,可得$\frac{4}{{a}^{2}}$-$\frac{4}{{b}^{2}}$=1,②
由①②可得a=$\sqrt{3}$,b=2$\sqrt{3}$,
则双曲线的方程为$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{12}$=1.
故选:B.
点评 本题考查双曲线的方程的求法,注意运用渐近线方程和待定系数法,考查方程思想和点到直线的距离公式,以及运算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
1.在△ABC中,内角A,B,C所对的边长分别为a,b,c.asinBcosC+csinBcosA=$\frac{1}{2}$b且a>b,则∠B=( )
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
18.若不等式|x-1|+|x+m|≤4的解集非空,则实数m的取值范围是( )
| A. | [-5,-3] | B. | [-3,5] | C. | [-5,3] | D. | [3,5] |
12.已知函数f(x)=$\left\{\begin{array}{l}-{x^2}+4,x<0\\ x{e^x},x≥0\end{array}$,若f(x1)=f(x2)(x1<x2),则$\frac{{f({x_2})}}{x_1}$的取值范围为( )
| A. | (-∞,0] | B. | [1,+∞) | C. | (-∞,0) | D. | (-∞,0)∪(0,+∞) |
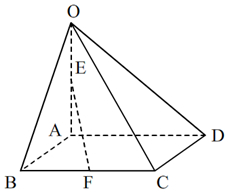 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点,
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点, 的是( )
的是( ) B.
B.
 D.
D.