题目内容
14.设函数f(x)=(x-a)lnx+b.(1)当a=0时,讨论函数f(x)在[$\frac{1}{e}$,+∞)上的零点个数;
(2)当a>1且函数f(x)在(1,e)上有极小值时,求实数a的取值范围.
分析 (1)先求导,求出函数的最小值,再根据最小值和0的关系分类讨论即可得到函数零点的个数,
(2)函数f(x)在(1,e)上有极小值时,则函数f(x)在(1,e)上不单调,先求导,构造函数g(x)=lnx+$\frac{x-a}{x}$,得到函数在(1,e)上单调递增,
即可以得到$\left\{\begin{array}{l}{g(1)<0}\\{g(e)>0}\end{array}\right.$,解得即可
解答 解:(1)当a=0时,f(x)=xlnx+b,
∴f′(x)=1+lnx≥0在[$\frac{1}{e}$,+∞)上恒成立,
∴f(x)在[$\frac{1}{e}$,+∞)单调递增,
∴f(x)min=f($\frac{1}{e}$)=-$\frac{1}{e}$+b,
当-$\frac{1}{e}$+b≤0时,即b≥$\frac{1}{e}$时,函数有唯一的零点,
当-$\frac{1}{e}$+b>0时,即b=$\frac{1}{e}$,函数没有零点,
(2)∵f′(x)=lnx+$\frac{x-a}{x}$,x∈(1,e)
令g(x)=lnx+$\frac{x-a}{x}$,
∴g′(x)=$\frac{1}{x}$+$\frac{a}{{x}^{2}}$>0恒成立,
∴g(x)在(1,e)上单调递增,
∴g(x)>g(1)=1-a,g(x)<g(e)=2-$\frac{a}{e}$,
∵函数f(x)在(1,e)上有极小值,
∴$\left\{\begin{array}{l}{g(1)=1-a<0}\\{g(e)=2-\frac{a}{e}>0}\end{array}\right.$,
解得1<a<2e,
故a的取值范围为(1,2e)
点评 本题考查了导数和函数的极值的关系以及函零点的个数问题,考查了学生分析问题,解决问题的能力,以及运算、分类讨论、转化的能力,属于中档题

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案| A. | x2-$\frac{3{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{12}$=1 | C. | x2-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{3}$=1 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分条件 | D. | 既不充分也不必要条件 |
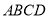 所在的平面与△
所在的平面与△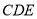 所在的平面交于
所在的平面交于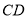 ,
,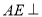 平面
平面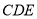 ,且
,且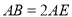 .
.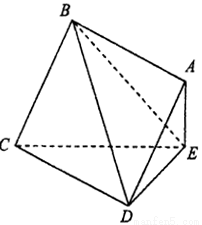
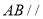 平面
平面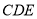 ;
;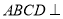 平面
平面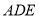 .
.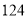 人,其中女性
人,其中女性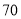 人,男性
人,男性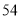 人.女性中有
人.女性中有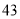 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有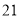 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动.
人主要的休闲方式是运动. 的倾斜角为( )
的倾斜角为( ) B.
B. C.
C. D.
D.