题目内容
已知函数f(x)＝Acos(
＋
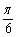)x∈R, 且f(
)＝
.
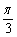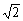（1）求A的值；
（2）设α,β∈[0,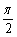 
], f(4α＋
π)＝―
, f(4β―
π)＝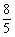
，求cos(α＋β)的值。
解：（1）由
∴A＝2
∴f(x)＝2cos(
＋)
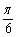（2）由f(4α＋
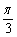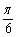)＝2cos(α＋＋)＝2cos(α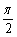＋)＝－2sinα＝－
∴sinα＝
由f(4β―π)＝2cosβ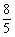＝，∴cosβ＝
由α,β∈(0, 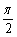)，则cosα＝
, sinβ＝
∴cos(α＋β)＝cosαcosβ－sinαsinβ
＝×－×＝
练习册系列答案
相关题目
(
)在区间
上取得最小值4,则
_ __.
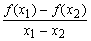＞0，则下列命题中正确的有 。
·
＝0，则
＝ 。
在R上可导，且
=
，则（ ）
B. 
C.
D. 不能确定