Question

设不等式组

x+y≤4 y-x≥0 x-1≥0

，表示的平面区域为D，若圆C：（x+1）²+（y+1）²=r²（r＞0）经过区域D上的点，则r的取值范围是（　　）

• A、[2

  2

  ，2

  5

  ]
• B、（2

  2

  ，3

  2

  ]
• C、（3

  2

  ，2

  5

  ]
• D、（0，2

  2

  ）∪（2

  5

  ，+∞）

Answer 1

考点：简单线性规划,圆的标准方程

专题：数形结合

分析：由约束条件作出可行域，求出圆C：（x+1）²+（y+1）²=r²的圆心坐标，数形结合可得r的取值范围．

解答： 解：由约束条件

x+y≤4 y-x≥0 x-1≥0

作出平面区域如图，

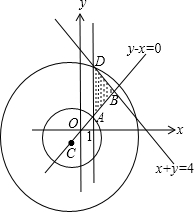
由C：（x+1）²+（y+1）²=r²，得圆心C（-1，-1），
联立

x=1 y-x=0

，得A（1，1），
联立

y-x=0 x+y=4

，得B（2，2），
联立

x=1 x+y=3

，得D（1，3）．
由图可知，半径r的最小值为|OA|=

(1+1)2+(1+1)2

=2

2

，
半径r的最大值为|OD|=

(1+1)2+(3+1)2

=2

5

．
故选：A．

点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，关键是正确作出可行域，是中档题．