题目内容
 (文科)已知如图,在三棱锥P-ABC中,顶点P在底面的投影H是△ABC的垂心.
(文科)已知如图,在三棱锥P-ABC中,顶点P在底面的投影H是△ABC的垂心.(Ⅰ)证明:PA⊥BC;
(Ⅱ)若PB=PC,BC=2,且二面角P-BC-A度数为60°,求三棱锥P-ABC的体积VP-ABC的值.
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:(Ⅰ)连接AH,并延长交BC于D,连接BH,并延长交AC于E,连接PD,证明H是△ABC的垂心,BC⊥面PAD,即可证明:PA⊥BC;
(Ⅱ)证明AB=AC,△ABD∽△BHD,求出△PAD的面积,即可求三棱锥P-ABC的体积VP-ABC的值.
(Ⅱ)证明AB=AC,△ABD∽△BHD,求出△PAD的面积,即可求三棱锥P-ABC的体积VP-ABC的值.
解答:
 (Ⅰ)证明:连接AH,并延长交BC于D,连接BH,并延长交AC于E,连接PD,
(Ⅰ)证明:连接AH,并延长交BC于D,连接BH,并延长交AC于E,连接PD,
由PH⊥面ABC,得PH⊥BC,
又H是△ABC的垂心,可得AD⊥BC,而PH∩AD=H,
则BC⊥面PAD,所以PA⊥BC;…(4分)
(Ⅱ)由(Ⅰ)知BC⊥面PAD,则BC⊥PD,
所以∠PDA为二面角P-BC-A的平面角,则有∠PDA=60°
由BC⊥PD,PB=PC,可知BD=DC,
又BC⊥AD,所以AB=AC
在△ABC中,因为H是垂心,由平面几何可知△ABD∽△BHD,
所以
=
,⇒AD•DH=BD2=1,则S△PAD=
AD•PH=
AD•DH•tan60°=
,
所以VP-ABC=
S△PAD•BC=
×
×2=
.…(9分)
 (Ⅰ)证明:连接AH,并延长交BC于D,连接BH,并延长交AC于E,连接PD,
(Ⅰ)证明:连接AH,并延长交BC于D,连接BH,并延长交AC于E,连接PD,由PH⊥面ABC,得PH⊥BC,
又H是△ABC的垂心,可得AD⊥BC,而PH∩AD=H,
则BC⊥面PAD,所以PA⊥BC;…(4分)
(Ⅱ)由(Ⅰ)知BC⊥面PAD,则BC⊥PD,
所以∠PDA为二面角P-BC-A的平面角,则有∠PDA=60°
由BC⊥PD,PB=PC,可知BD=DC,
又BC⊥AD,所以AB=AC
在△ABC中,因为H是垂心,由平面几何可知△ABD∽△BHD,
所以
| AD |
| BD |
| BD |
| DH |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
所以VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 3 |
点评:本题考查线面垂直、线线垂直,考查三棱锥P-ABC的体积,考查学生分析解决问题的能力,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
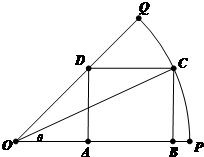 已知OPQ是半径为1,圆心角为
已知OPQ是半径为1,圆心角为 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2