题目内容
4.若△ABC外接圆直径为2,A=75°,B=45°,则△ABC的面积为$\frac{3+\sqrt{3}}{4}$.分析 利用圆周角定理得出三个圆心角的度数,将△ABC分解成三个小三角形求面积.
解答  解:设△ABC的外心为O,∵B=45°,A=75°,∴C=180°-A-B=60°.
解:设△ABC的外心为O,∵B=45°,A=75°,∴C=180°-A-B=60°.
∴∠AOC=2B=90°,∠BOC=2A=150°,∠AOB=2C=120°,
∵OA=OB=OC=1,
∴S△ABC=S△AOC+S△BOC+S△AOB=$\frac{1}{2}$sin90°+$\frac{1}{2}$sin150°+$\frac{1}{2}$sin120°=$\frac{3+\sqrt{3}}{4}$.
故答案为$\frac{3+\sqrt{3}}{4}$.
点评 本题考查了三角形外接圆的性质,面积计算,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
12.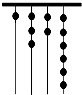 原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?( )
原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?( )
 原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?( )
原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?( )| A. | 1326 | B. | 510 | C. | 429 | D. | 336 |
19.已知三棱锥ABCD中,AB⊥CD,且AB与平面BCD成60°角.当$\frac{{S}_{△BCD}}{{S}_{△ACD}}$的值取到最大值时,二面角A-CD-B的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
16.已知$\overrightarrow{a}$$⊥\overrightarrow{b}$,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,且3$\overrightarrow{a}$$+2\overrightarrow{b}$与λ$\overrightarrow{a}$$-\overrightarrow{b}$垂直,则λ等于( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | ±$\frac{3}{2}$ | D. | 1 |
12.已知命题p:-1≤x≤5,命题q:(x-5)(x+1)<0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
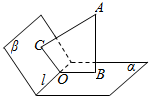 如图所示,在二面角α-l-β内有一点A,过A作AB⊥α于B,作AC⊥β于C,如果∠BAC=25°,那么二面角α-l-β是多少度.
如图所示,在二面角α-l-β内有一点A,过A作AB⊥α于B,作AC⊥β于C,如果∠BAC=25°,那么二面角α-l-β是多少度. 如图所示,抛物线y2=4x的焦点为F,动点T(-1,m),过F作TF的垂线交抛物线于P,Q两点,弦PQ的中点为N.
如图所示,抛物线y2=4x的焦点为F,动点T(-1,m),过F作TF的垂线交抛物线于P,Q两点,弦PQ的中点为N.