题目内容
已知抛物线 y2=2x,直线l过点(0,2)与抛物线交于M,N两点,以线段MN的长为直径的圆过坐标原点O,求直线l的方程.
y2=2x,直线l过点(0,2)与抛物线交于M,N两点,以线段MN的长为直径的圆过坐标原点O,求直线l的方程.
解 由题意知直线l的斜率存在,
设为k,则直线l的方程为y=kx+2,
解方程组 ,
,
消去x得ky2-2y+4=0,
Δ=4-16k>0⇒k< (k≠0),
(k≠0),
设M(x1,y1),N(x2,y2),
则y1+y2= ,y1y
,y1y 2=
2= ,
,
 ⇒x1x2=
⇒x1x2= (y1y2)2=
(y1y2)2= .
.
OM⊥ON⇒kOM·kON=-1,
∴x1x2+y1y2=0,
∴ +
+ =0,解得k=-1.
=0,解得k=-1.
所以所求直线方程为y=-x+2,
即x+y-2=0.

练习册系列答案
相关题目
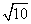 ,0),则双曲线的方程是_ ___________.
,0),则双曲线的方程是_ ___________.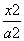 -
-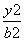 =1 (a>0,b>0)的左、右焦点分别是F1,F2,过F1作倾斜角为30°的直 线交双曲线右支于M点,若MF2垂直于x轴,则双曲线的离心率为________.
=1 (a>0,b>0)的左、右焦点分别是F1,F2,过F1作倾斜角为30°的直 线交双曲线右支于M点,若MF2垂直于x轴,则双曲线的离心率为________.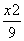 -
-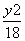 =1的焦点作弦MN,若MN=48,则此弦的倾斜角为________.
=1的焦点作弦MN,若MN=48,则此弦的倾斜角为________. 若直线l:y=kx+m与椭圆
若直线l:y=kx+m与椭圆 +
+ =1相交于A、B两点(A、B不是左、右顶点),A2为椭圆的右顶点且AA2⊥BA2,求证:直线l过定点.
=1相交于A、B两点(A、B不是左、右顶点),A2为椭圆的右顶点且AA2⊥BA2,求证:直线l过定点. ,b=
,b= ,c=
,c= ,则a,b,c的大小关系为( )
,则a,b,c的大小关系为( )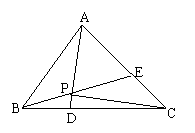 如图,在正ΔABC中,点D、E分别在边BC, AC上,且
如图,在正ΔABC中,点D、E分别在边BC, AC上,且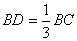 ,
,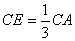 ,AD,BE相交于点P.
,AD,BE相交于点P. 某班级从甲乙两位同学选派一人参加数学竞赛,老师对他们平时的10次模拟测试成绩(单位:分)进行了记录如下:
某班级从甲乙两位同学选派一人参加数学竞赛,老师对他们平时的10次模拟测试成绩(单位:分)进行了记录如下: