题目内容
判断命题“已知a、x为实数,如果关于x的不等式x2+(2a+1)x+a2+2≤0的解集非空,则a≥1”的逆否命题的真假.
解 方法一 (直接法)
逆否命题:已知a、x为实数,如果a<1,则关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集.
判断如下:
二次函数y=x2+(2a+1)x+a2+2图象的开口向上,
判别式Δ=(2a+1)2-4(a2+2)=4a-7.
∵a<1,∴4a-7<0.
即二次函数y=x2+(2a+1)x+a2+2与x轴无交点,∴关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集,故逆否命题为真.
方法二 (先判断原命题的真假)
∵a、x为实数,且关于x的不等式x2+(2a+1)x+a2+2≤0的解集非空,
∴Δ=(2a+1)2-4(a2+2)≥0,即4a-7≥0,
解得a≥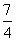 ,∵a≥
,∵a≥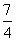 >1,
>1,
∴原命题为真.
又∵原命题与其逆否命题等价,∴逆否命题为真.
方法三 (利用集合的包含关系求解)
命题p:关于 x的不等式x2+(2a+1)x+a2+2≤0有非空解集.
x的不等式x2+(2a+1)x+a2+2≤0有非空解集.
命题q:a≥1.
∴p:A={a|关于x的不等式x2+(2a+1)x+a2+2≤0有实数解}={a|(2a+1)2-4(a2+2)≥0}=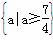 ,
,
q:B={a|a≥1}.
∵A⊆B,∴“若p,则q”为真,
∴“若p,则q”的逆否命题“若綈q,则綈p”为真.
即原命题的逆否命题为真.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 =
=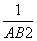 +
+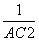 成立.那么在四面体A-BCD中,
成立.那么在四面体A-BCD中, 类比上述结论,你能得到怎样的猜想,说明猜想是否正确及并给出理由.
类比上述结论,你能得到怎样的猜想,说明猜想是否正确及并给出理由. (其中x∈R且x≠
(其中x∈R且x≠ ),求证:经过这个
),求证:经过这个 函数图象上任意两个不同点的直线不平行于x轴.
函数图象上任意两个不同点的直线不平行于x轴. ________.(填序号)
________.(填序号)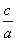 >
>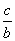 ”的逆否命题;
”的逆否命题; -2x0-1≤0,则命题p∧綈q是真命题.
-2x0-1≤0,则命题p∧綈q是真命题. 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式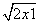 <1+ax对一切正实数均成立.如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围.
<1+ax对一切正实数均成立.如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围. y2=2x,直线l过点(0,2)与抛物线交于M,N两点,以线段MN的长为直径的圆过坐标原点O,求直线l的方程.
y2=2x,直线l过点(0,2)与抛物线交于M,N两点,以线段MN的长为直径的圆过坐标原点O,求直线l的方程.