题目内容
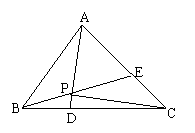如图，在正ΔABC中，点D、E分别在边BC, AC上,且
,
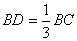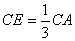，AD，BE相交于点P.
求证：(I) 四点P、D、C、E共 圆；
(II) AP ⊥CP。
证明：（I）在
中，由
知：
≌
，………………2分
即
.
所以四点
共圆；………………5分
（II）如图，连结
.
在
中，
,
,
由正弦定理知
.………………8分
由四点共圆知，
,
所以
………………10分
练习册系列答案
相关题目
题目内容
如图，在正ΔABC中，点D、E分别在边BC, AC上,且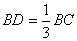,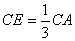，AD，BE相交于点P.
求证：(I) 四点P、D、C、E共 圆；
(II) AP ⊥CP。
证明：（I）在中，由知：
≌，………………2分
即.
所以四点共圆；………………5分
（II）如图，连结.
在中，,,
由正弦定理知.………………8分
由四点共圆知，,
所以………………10分
的定义域为R；命题q：不等式
<1＋ax对一切正实数均成立．如果命题p或q为真命题，命题p且q为假命题，求实数a的取值范围．
y2＝2x，直线l过点(0,2)与抛物线交于M，N两点，以线段MN的长为直径的圆过坐标原点O，求直线l的方程．
满足对任意
B. 
C. 
D. 
.
满足
(1)=4,且
，则不等式
的解集为
B. 
C. 
D. 
，
满足
，
，且
，则
C． 2 D．
若不等式
的解集是
， 求不等式
的解集.