题目内容
17.若抛物线x2=2py(p>0)的焦点与椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的一个顶点重合,则该抛物线的焦点到准线的距离为4.分析 求出椭圆的顶点坐标,得到抛物线的焦点坐标,求出P即可得到结果.
解答 解:抛物线x2=2py(p>0)的焦点与椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的一个顶点(0,2)重合,
抛物线的开口向上,焦点坐标(0,2),
可得p=4,则该抛物线的焦点到准线的距离为:p=4.
故答案为:4.
点评 本题考查椭圆的简单性质以及抛物线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
8.设函数f(x)=$\left\{\begin{array}{l}{lo{g}_{9}x,x>0}\\{{4}^{-x}+\frac{3}{2},x≤0}\end{array}\right.$,则f(27)+f(-log43)的值为( )
| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
9.“-3<a<1”是“存在x∈R,使得|x-a|+|x+1|<2”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
13.下列框图中,可作为流程图的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
14.设随机变量X~N(2,52),且P(X≤0)=P(X≥a-2),则实数a的值为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
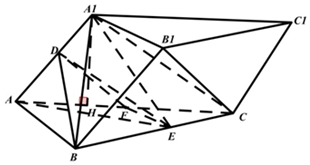 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.