题目内容
等差数列{an}中，a2+a4=8，a3+a4=3，那么它的公差是（ ）
| A、4 | B、-5 | C、6 | D、7 |
考点：等差数列的通项公式
专题：
分析：由已知得
，由此能求出公差．
|
解答：
解：∵等差数列{an}中，a2+a4=8，a3+a4=3，
∴
，
解得d=-5．
故选：B．
∴
|
解得d=-5．
故选：B．
点评：本题考查等差数列的公差的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
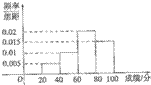某班的全体学生参加某项技能测试，成绩的频率分布直方图如图，数据的分组依次为：[20，40），[40，60），[60，80），[80，100]，若不低于80分的人数是8，则该班的学生人数是（ ）| A、45 | B、50 | C、55 | D、60 |
在△ABC中，tanA+tanB+tanC＞0是△ABC是锐角三角形的（ ）
| A、既不充分也不必要条件 |
| B、充分必要条件 |
| C、必要不充分条件 |
| D、充分不必要条件 |
已知正项等比数列{an}中，a5，a95为方程x2+10x+16=0的两根，则a20•a50•a80的值为（ ）
| A、256 | B、±256 |
| C、64 | D、±64 |