题目内容
4.某革命老区为带动当地经济的发展,实现经济效益与社会效益双赢,精心准备了三个独立的方案;方案一:红色文化体验专营经济带,案二:农家乐休闲区专营经济带,方案三:爱国主义教育基础,通过委托民调机构对这三个方案的调查,结果显示它们能被民众选中的概率分别为$\frac{2}{5}$,$\frac{3}{4}$,$\frac{1}{3}$.(1)求三个方案至少有两个被选中的概率;
(2)记三个方案被选中的个数为?,试求?的期望.
分析 记三个方案记为甲、乙、丙,被选中的事件分别为A,B,C,则P(A)=$\frac{2}{5}$,P(B)=$\frac{3}{4}$,P(C)=$\frac{1}{3}$
(1)“只有两个方案被选中”可分为三种情形:①甲未被选中,乙、丙被选中,②乙未被选中,甲、丙被选中,③丙未被选中,甲、乙被选中,3个方案被选中,概率为$\frac{2}{5}$×$\frac{3}{4}$×$\frac{1}{3}$=$\frac{1}{10}$从而求概率;
(2)由题意可知?的可能取值为0,1,2,3.求其概率从而求数学期望.
解答 解:记三个方案记为甲、乙、丙,被选中的事件分别为A,B,C,则P(A)=$\frac{2}{5}$,P(B)=$\frac{3}{4}$,P(C)=$\frac{1}{3}$.
(1)“只有两个方案被选中”可分为三种情形:
①甲未被选中,乙、丙被选中,概率为P1=$\frac{3}{5}$×$\frac{3}{4}$×$\frac{1}{3}$=$\frac{3}{20}$.
②乙未被选中,甲、丙被选中,概率为P2=$\frac{2}{5}$×$\frac{1}{4}$×$\frac{1}{3}$=$\frac{1}{30}$.
③丙未被选中,甲、乙被选中,概率为P3=$\frac{2}{5}$×$\frac{3}{4}$×$\frac{2}{3}$=$\frac{1}{5}$.
以上三种情况是互斥的.因此只有两个方案被选中的概率为P=$\frac{23}{60}$.
3个方案被选中,概率为$\frac{2}{5}$×$\frac{3}{4}$×$\frac{1}{3}$=$\frac{1}{10}$,
∴三个方案至少有两个被选中的概率为$\frac{23}{60}$+$\frac{1}{10}$=$\frac{29}{60}$;
(2)由题意可知?的可能取值为0,1,2,3.
P(?=0)=$\frac{2}{5}$×$\frac{3}{4}$×$\frac{1}{3}$=$\frac{1}{10}$;
P(?=1)=$\frac{2}{5}$×$\frac{1}{4}$×$\frac{2}{3}$+$\frac{2}{3}$×$\frac{3}{5}$×$\frac{3}{4}$+$\frac{3}{5}$×$\frac{1}{4}$×$\frac{1}{3}$=$\frac{25}{60}$;
由(1)知P(?=2)=$\frac{23}{60}$;
P(?=3)=$\frac{2}{5}$×$\frac{3}{4}$×$\frac{1}{3}$=$\frac{1}{10}$.
故E?=0×$\frac{1}{10}$+1×$\frac{25}{60}$+2×$\frac{23}{60}$+3×$\frac{1}{10}$=$\frac{89}{60}$.
点评 本题考查了数学期望的求法,考查概率的计算,属于中档题.

 字词句段篇系列答案
字词句段篇系列答案| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
| A. | (-1,7),(5,2) | B. | (-1,7),(-5,2) | C. | (1,4),(5,2) | D. | (-1,4),(-5,2) |
| A. | cosC | B. | -cosC | C. | sinC | D. | -sinC |
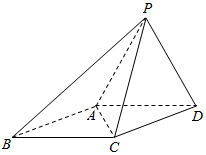 如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.