��Ŀ����
16����֪$\overrightarrow{a}$��$\overrightarrow{b}$��������λ������������|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2������|$\overrightarrow{a}$-$\overrightarrow{b}$|��ֵ��
������$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ60�㣬��������$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{b}$��$\overrightarrow{n}$=$\overrightarrow{a}$-3$\overrightarrow{b}$�ļнǵ�����ֵ��
���� ������ƽ����������������ģ����ʽ�������$\overrightarrow{a}$•$\overrightarrow{b}$��ֵ�������|$\overrightarrow{a}$-$\overrightarrow{b}$|��
������ƽ����������������нǹ�ʽ���������$\overrightarrow{m}$��$\overrightarrow{n}$�нǵ�����ֵ��
��� �⣺����$\overrightarrow{a}$��$\overrightarrow{b}$��������λ������
��|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2ʱ��${��\overrightarrow{a}-2\overrightarrow{b}��}^{2}$=${\overrightarrow{a}}^{2}$-4$\overrightarrow{a}$•$\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$=1-4$\overrightarrow{a}$•$\overrightarrow{b}$+4=4��
��$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{4}$��
��${��\overrightarrow{a}-\overrightarrow{b}��}^{2}$=${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=1-2��$\frac{1}{4}$+1=$\frac{3}{2}$��
��|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{\frac{3}{2}}$=$\frac{\sqrt{6}}{2}$��
������$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ60�㣬��$\overrightarrow{a}$•$\overrightarrow{b}$=1��1��cos60��=$\frac{1}{2}$��
������$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{b}$��$\overrightarrow{n}$=$\overrightarrow{a}$-3$\overrightarrow{b}$��
��$\overrightarrow{m}$•$\overrightarrow{n}$=${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}$•$\overrightarrow{b}$-3${\overrightarrow{b}}^{2}$=1-2��$\frac{1}{2}$-3��1=-3��
|$\overrightarrow{m}$|=$\sqrt{{\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{1+2��\frac{1}{2}+1}$=$\sqrt{3}$��
|$\overrightarrow{n}$|=$\sqrt{{\overrightarrow{a}}^{2}-6\overrightarrow{a}•\overrightarrow{b}+{9\overrightarrow{b}}^{2}}$=$\sqrt{1-6��\frac{1}{2}+9}$=$\sqrt{7}$��
��$\overrightarrow{m}$��$\overrightarrow{n}$�ļнǦȵ�����ֵΪ
cos��=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|��|\overrightarrow{n}|}$=$\frac{-3}{\sqrt{3}��\sqrt{7}}$=-$\frac{\sqrt{21}}{7}$��
���� ���⿼����ƽ����������������ģ����ʽ�Լ��нǹ�ʽ��Ӧ�����⣬�ǻ�����Ŀ��

 ��У����ϵ�д�
��У����ϵ�д�| A�� | 11110 | B�� | 10101 | C�� | 10011 | D�� | 10001 |
| A�� | 1 | B�� | 2 | C�� | $\frac{{2\sqrt{3}}}{3}$ | D�� | $\sqrt{3}$ |
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
| A�� | 5 | B�� | {5} | C�� | ∅ | D�� | {1��2��3��4} |
| A�� | g��x��=x2 | B�� | $g��x��=\frac{1}{x}$ | C�� | g��x��=x3 | D�� | $g��x��={x^{\frac{1}{2}}}$ |
| A�� | ������x0��R��$x_0^2+{x_0}+1��0$ | B�� | ?x0��R��$x_0^2+{x_0}+1��0$ | ||
| C�� | ?x��R��x2+x+1��0 | D�� | ?x��R��x2+x+1��0 |
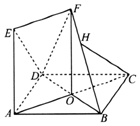 ��ͼ��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O���ı���OAEFΪ���Σ�ƽ��OAEF��ƽ��ABCD��AB=AE��
��ͼ��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O���ı���OAEFΪ���Σ�ƽ��OAEF��ƽ��ABCD��AB=AE��