题目内容
4.在四个函数y=sin|2x|,y=|sinx|,y=sin(2x+$\frac{π}{6}$),y=tan(2x-$\frac{π}{4}$)中,最小正周期为π的所有函数个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用周期函数的概念,结合三角函数的图象与性质,对题目中的四个函数的最小正周期进行分析、判断即可.
解答 解:函数y=sin|2x|不是周期函数,不满足条件;
令y=f(x)=|sinx|,则f(x+π)=|sin(x+π)|=|-sinx|=|sinx|=f(x),
∴函数y=|sinx|是最小正周期为π的函数,满足条件;
又函数y=sin(2x+$\frac{π}{6}$)的最小正周期为T=$\frac{2π}{2}$=π,满足条件;
函数y=tan(2x-$\frac{π}{4}$)的最小正周期为T=$\frac{π}{2}$,不满足条件.
综上,以上4个函数中,最小正周期为π有2个.
故选:B.
点评 本题考查了求三角函数的最小正周期性的应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.抛物线x2=-6by的准线与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右支分别交于B、C两点,A为双曲线的右顶点,O为坐标原点,若∠AOC=∠BOC,则双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 3 | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
12.假设行列式的计算公式:$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,若f(x)=$|\begin{array}{l}{x}&{x}\\{3}&{{x}^{2}}\end{array}|$,则函数f(x)的单调减区间为( )
| A. | $(-\sqrt{3},\sqrt{3})$ | B. | (-1,1) | C. | $(-\sqrt{2},\sqrt{2})$ | D. | (-2,2) |
14.如图,网格纸上的小正方形边长为1,粗线或虚线表示一个棱柱的三视图,则此棱柱的侧面积为( )
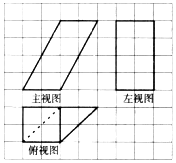

| A. | 16+4$\sqrt{5}$ | B. | 20+4$\sqrt{5}$ | C. | 16+8$\sqrt{5}$ | D. | 8+12$\sqrt{5}$ |