题目内容
已知函数y=2x+
,求函数值域(用画图法解答).
| 1-x2 |
考点:函数的值域
专题:函数的性质及应用
分析:把原函数移项平方,把函数转化成关于x的一元二次方程,利用二次函数的性质结合图象,确定y的范围.
解答:
解:对函数解析式恒等变形得(y-2x)2=1-x2,(-1≤x≤1),
整理得5x2-4xy+y2-1=0,
令f(x)=5x2-4xy+y2-1,则此函数在区间[-1,1]上有零点,需
解得-
≤y≤
,

整理得5x2-4xy+y2-1=0,
令f(x)=5x2-4xy+y2-1,则此函数在区间[-1,1]上有零点,需
|
| 5 |
| 5 |

点评:本题主要考查了二次函数的性质,函数的值域问题.解题过程中运用了数形结合的思想.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
不等式组
,表示的平面区域为Ω,直线y=kx-1与区域Ω有公共点,则实数k的取值范围为( )
|
| A、(0,3] |
| B、[-1,1] |
| C、(-∞,3] |
| D、[3,+∞) |
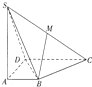 四棱锥S-ABCD中,SA⊥平面ABCD,底面四边形ABCD为直角梯形,AB∥CD,AD⊥DC,SA=AD=DC=2,AB=1.
四棱锥S-ABCD中,SA⊥平面ABCD,底面四边形ABCD为直角梯形,AB∥CD,AD⊥DC,SA=AD=DC=2,AB=1.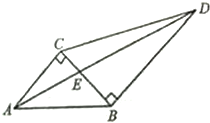 如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.
如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.