题目内容

19．若命题“直线y=kx+2与圆x2+y2=1有公共点”是假命题，则实数k的取值范围是（-$\sqrt{3}，\sqrt{3}$）．

分析 由题意可知：圆心（0，0）到直线y=kx+2距离d=$\frac{丨2丨}{\sqrt{1+{k}^{2}}}$≤1，由命题P“直线y=kx+2与圆x2+y2=1有公共点”是假命题，则￢P为真，即可求得k的取值范围．

解答 解：由题意可知：直线y=kx+2与圆x2+y2=1有公共点，即圆心到直线y=kx+2距离d≤1，
∴圆心（0，0）到直线y=kx+2距离d=$\frac{丨2丨}{\sqrt{1+{k}^{2}}}$≤1，解得：k≥$\sqrt{3}$或k≤-$\sqrt{3}$，
由命题P“直线y=kx+2与圆x2+y2=1有公共点”是假命题，则￢P为真，
∴-$\sqrt{3}$＜k＜$\sqrt{3}$，
实数k的取值范围（-$\sqrt{3}$，$\sqrt{3}$），
故答案为：（-$\sqrt{3}$，$\sqrt{3}$）．

点评 本题考查直线与圆的位置关系，考查点到直线的距离公式，考查命题的真假性的判断，考查计算能力，属于中档题．

练习册系列答案
相关题目
15．设函数$f（x）=\left\{{\begin{array}{l}{{{log}_2}x，x＞0}\\{{{log}_{0.5}}（-x），x＜0}\end{array}}\right.$．
（I）求$f（f（-\frac{1}{4}））$的值；
（II）若f（a）＞f（-a），求实数a的取值范围．
16．不等式（x+$\frac{1}{2}$）（$\frac{3}{2}$-x）≥0的解集是（　　）
A．{x|-$\frac{1}{2}$≤x≤$\frac{3}{2}$}B．{x|x≤-$\frac{1}{2}$或x≥$\frac{3}{2}$}C．{x|x＜-$\frac{1}{2}$或x＞$\frac{3}{2}$}D．{x|-$\frac{1}{2}$＜x＜$\frac{3}{2}$}
7．若x轴为曲线f（x）=x3-ax-$\frac{1}{4}$的切线，则a=（　　）
A．$\frac{3}{4}$B．$-\frac{3}{4}$C．$\frac{1}{2}$D．-$\frac{1}{2}$
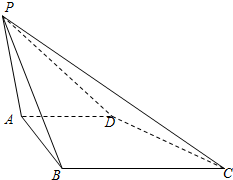14．如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，侧面PAD同时垂直侧面PAB与侧面PDC．若PA=AB=AD=$\frac{{\sqrt{3}}}{3}$PB，则$\frac{BC}{AD}$=$\frac{3}{2}$，直线PC与底面ABCD所成角的正切值为$\frac{\sqrt{6}}{6}$．
4．在△ABC中，角A，B，C的对边分别是a，b，c，且a=1，b=$\sqrt{3}$，A=30°．
（1）求sinB的值；
（2）求cosC的值．
11．已知函数f（x）=x2+mx+n（m，n∈R），f（0）=f（1），且方程f（x）=x有两个相等的实数根．
（1）求函数f（x）的解析式；
（2）当x∈（0，2）时，求函数f（x）的值域．
8．若X是一个非空集合，M是一个以X的某些子集为元素的集合，且满足：
（1）X∈M，Φ∈M；
（2）对于X的任意子集A，B，当A∈M，B∈M时，A∪B∈M，A∩B∈M．则称M是集合X的一个“M-集合类”．
例如：M={Φ，{b}，{c}，{b，c}，{a，b，c}}是集合X={a，b，c}的一个“M-集合类”．已知集合X={a，b，c}，则所有含{b，c}的“M-集合类”的个数为10．
9．若α为第三象限角，则$\sqrt{1-sin{α}^{2}}$的结果为（　　）
A．sinαB．-sinαC．cosαD．-cosα

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网