题目内容
设正数x，y满足
，则4x+6y-1的最大值为（ ）
|
| A、3 | B、4 | C、5 | D、6 |
考点：简单线性规划
专题：不等式的解法及应用
分析：画出约束条件表示的可行域，求出最优解，然后求解最值．
解答：
解：如图，作出
的可行域，由
，解得
由图及目标函数得最优解为P（1，0.5），将x=1，y=0.5代入
目标函数z=4x+6y-1得6，
故选D
解：如图，作出
|
|
|
由图及目标函数得最优解为P（1，0.5），将x=1，y=0.5代入
目标函数z=4x+6y-1得6，
故选D
点评：本题考查线性规划的应用，正确画出可行域是解题的关键，考查基本知识的应用．
练习册系列答案
阅读快车系列答案
相关题目
已知F1，F2是椭圆和双曲线的公共焦点，P是它们的一个公共点，且∠F1PF2=
，则椭圆和双曲线的离心率的乘积的最小值为（ ）
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知：p：x＜k，q：x≤1，如果p是q的充分不必要条件，则k的取值范围是（ ）
| A、[2，+∞） |
| B、（2，+∞） |
| C、（-∞，-1） |
| D、（-∞，1] |
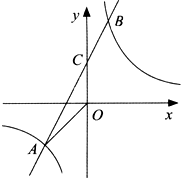如图，已知A（n，-2），B（1，4）是一次函数y=kx+b的图象和反比例函数y=