题目内容
7. 如图,已知F(1,0)为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,离心率$\frac{\sqrt{2}}{2}$.
如图,已知F(1,0)为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,离心率$\frac{\sqrt{2}}{2}$.(1)求椭圆的方程;
(2)P为椭圆上一点,椭圆在P点处的切线与直线x=c和右准线x=$\frac{{a}^{2}}{c}$分别交于点M,N.
①若P(0,1),求$\frac{MF}{NF}$的值;
②探究当P在椭圆上移动时,$\frac{MF}{NF}$的值是否为定值?若是,求出此定值,否则,说明理由.
分析 (1)由题意c=1,a=$\sqrt{2}$,b=1,即可求椭圆的方程;
(2)①若P(0,1),则M(1,1),N(2,1),即可求$\frac{MF}{NF}$的值;
②求出切线方程,利用两点间的距离公式,再代入化简,即可得出结论.
解答 解:(1)由题意c=1,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a2-b2=c2,
解得a=$\sqrt{2}$,b=1,
∴椭圆的方程$\frac{{x}^{2}}{2}+{y}^{2}$=1;
(2)①若P(0,1),则M(1,1),N(2,1),
∴$\frac{MF}{NF}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$;
②设P(m,n),则切线方程为$\frac{mx}{2}$+ny=1,
设方程为y=kx+t,则k=-$\frac{m}{2n}$,t=-$\frac{1}{n}$,
∴t2=2k2+1,∴M(1,k+b),N(2,1-2k+b),
∴($\frac{MF}{NF}$)2=$\frac{{k}^{2}+{b}^{2}+2kb}{4{k}^{2}+4kb+{b}^{2}+1}$=$\frac{1}{2}$,
∴$\frac{MF}{NF}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
综上所述,当P在椭圆上移动时,$\frac{MF}{NF}$的值是定值$\frac{\sqrt{2}}{2}$.
点评 本题考查椭圆的方程与性质,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知P是直线kx+4y-10=0(k>0)上的动点,是圆C:x2+y2-2x+4y+4=0的两条切线,A,B是切点,C是圆心,若四边形PACB面积的最小值为$2\sqrt{2}$,则k的值为( )
| A. | 3 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{15}{2}$ |
12.若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽样5000件进行检测,结果发现有50件不合格.计算这50件不合格的直径长与标准值的差(单位:mm),将所得数据进行分组,得出频率分布表如下:
(1)表格①②③④缺少的数据分别是什么?
(2)估计该厂生产的此种产品中,不合格的直径长与标准值的差落在(1,3]内的概率;
(3)现对该厂这种产品的某批次进行检查,结果发现有20件产品不合格,据此估算这批产品中合格品的件数.
| 分组 | 频数 | 频率 |
| [-3,-2) | ① | 0.10 |
| [-2,-1) | 8 | 0.16 |
| (1,2] | ② | 0.50 |
| (2,3] | 10 | ③ |
| (3,4] | ④ | 0.04 |
| 合计 | 50 | 1.00 |
(2)估计该厂生产的此种产品中,不合格的直径长与标准值的差落在(1,3]内的概率;
(3)现对该厂这种产品的某批次进行检查,结果发现有20件产品不合格,据此估算这批产品中合格品的件数.
2.若函数f(x)=x|x-a|在[2,+∞)上单调递增,则实数a的取值范围为( )
| A. | (-∞,+∞) | B. | (-2,+∞) | C. | (0,+∞) | D. | (-∞,2] |
12.已知等差数列{an}的前n项和为Sn,a2=2,S5=15,则数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前2017项和为( )
| A. | $\frac{2016}{2017}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
16.如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log3(x+1)的解集是( )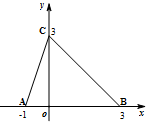

| A. | {x|-1≤x≤2} | B. | {x|-1<x≤2} | C. | {x|-1<x≤0} | D. | {x|-1<x≤3} |
17.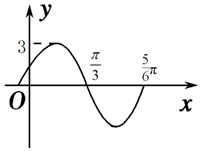 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | f(x)的一个对称中心为$(\frac{4π}{3},0)$ | B. | f(x)的图象关于直线$x=-\frac{1}{12}π$ 对称 | ||
| C. | f(x)在$[-π,-\frac{π}{2}]$上是增函数 | D. | f(x)的周期为$\frac{π}{2}$ |