在△ABC中.A.B.C的对边分别为$a.b.c.\overrightarrow m=.\overrightarrow b=$.且$\overrightarrow m•\overrightarrow n=2acosB$．(1)求B的大小,(2)若△ABC的面积为$2\sqrt{3}$.且a+c=6.求b．题目和参考答案——青夏教育精英家教网——

题目内容

19．在△ABC中，A，B，C的对边分别为$a，b，c，\overrightarrow m=（{a，0}），\overrightarrow b=（{1，cosB}）$，且$\overrightarrow m•\overrightarrow n=2acosB$．
（1）求B的大小；
（2）若△ABC的面积为$2\sqrt{3}$，且a+c=6，求b．

分析（1）根据$\overrightarrow{m}$•$\overrightarrow{n}$=2acosB，得a=2acosB，求出B的值即可；（2）根据三角形的面积求出ac=8，由a+c=6，联立方程组，求出a，c的值，根据余弦定理求出b的值即可．

解答解：（1）由$\overrightarrow{m}$=（a，0），$\overrightarrow{n}$=（1，cosB），
$\overrightarrow{m}$•$\overrightarrow{n}$=2acosB，得a=2acosB，
故cosB=$\frac{1}{2}$，得B=$\frac{π}{3}$；
（2）S_△ABC=$\frac{1}{2}$acsinB=2$\sqrt{3}$得ac=8，
联立$\left\{\begin{array}{l}{ac=8}\\{a+c=6}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=4}\\{c=2}\end{array}\right.$或$\left\{\begin{array}{l}{a=2}\\{c=4}\end{array}\right.$，
由余弦定理得b²=16+4-8=12，
解得：b=2$\sqrt{3}$．

点评本题考查了向量的乘法，考查余弦定理的应用，是一道中档题．

练习册系列答案

3年中考试卷汇编中考考什么系列答案

北舟文化考点扫描系列答案

金牌教辅中考真题专项训练系列答案

尚文教育首席中考系列答案

新领程小学毕业升学总复习全真模拟试卷系列答案

四川本土好学生寒假总复习系列答案

学成教育中考一二轮总复习阶梯试卷系列答案

蓉城中考系列答案

假期总动员寒假作业假期最佳复习计划系列答案

庠序文化中考必备中考试题汇编系列答案

相关题目

3．已知函数$f（x）=2\sqrt{3}sinxcosx+2{cos^2}x-1$，则下列说法正确的是（　　）

	A．	$（\frac{7π}{12}，0）$是函数y=f（x）的对称中心		B．	$x=\frac{7π}{12}$是函数y=f（x）的对称轴
	C．	$（-\frac{π}{12}，0）$是函数y=f（x）的对称中心		D．	$x=-\frac{π}{12}$是函数y=f（x）的对称轴

4．若坐标原点在圆x²+y²-2mx+2my+2m²-4=0的内部，则实数m的取值范围是（　　）

（-$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{2}}{2}$）

（-$\sqrt{3}$，$\sqrt{3}$）

（-$\sqrt{2}$，$\sqrt{2}$）

如图，已知F（1，0）为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点，离心率$\frac{\sqrt{2}}{2}$．
（1）求椭圆的方程；
（2）P为椭圆上一点，椭圆在P点处的切线与直线x=c和右准线x=$\frac{{a}^{2}}{c}$分别交于点M，N．
①若P（0，1），求$\frac{MF}{NF}$的值；
②探究当P在椭圆上移动时，$\frac{MF}{NF}$的值是否为定值？若是，求出此定值，否则，说明理由．

14．已知函数$f（x）=\left\{\begin{array}{l}（{3-a}）x-1，x≤5\\{a^{x-4}}，x＞5\end{array}\right.（{a＞0，a≠1}）$，数列{a_n}满足${a_n}=f（n）（{n∈{N^*}}）$，且{a_n}是单调递增数列，则实数a的取值范围是（　　）

$[{\frac{7}{3}，3}）$

$（{1，\frac{7}{3}}]$

4．若偶函数y=f（x）（x∈R）满足f（1+x）=f（1-x），且当x∈[-1，0]时，f（x）=x²，则函数g（x）=f（x）-|lgx|的零点个数为10个．

如图正四面体（所有棱长都相等）D-ABC中，动点P在平面BCD上，且满足∠PAD=30°，若点P在平面ABC上的射影为P′，则sin∠P′AB的最大值为（　　）

$\frac{2\sqrt{7}}{7}$

$\frac{\sqrt{6}-\sqrt{2}}{4}$

$\frac{\sqrt{3}}{2}$

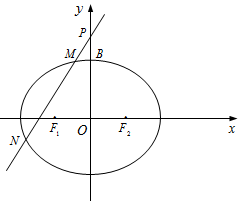已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的左，右焦点分别为F₁，F₂，上顶点为B．Q为抛物线y²=24x的焦点，且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$，$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过定点P（0，4）的直线l与椭圆C交于M，N两点（M在P，N之间），设直线l的斜率为k（k＞0），在x轴上是否存在点A（m，0），使得以AM，AN为邻边的平行四边形为菱形？若存在，求出实数m的取值范围；若不存在，请说明理由．

9．函数f（x）=$\sqrt{lo{g}_{\frac{1}{2}}（2x+1）}$的定义域为（　　）

（-$\frac{1}{2}$，0）

（-$\frac{1}{2}$，0]

（-$\frac{1}{2}$，+∞）