题目内容
1.已知公差不为0的等差数列{an}的首项a1为a(a∈R),且$\frac{1}{a_1},\frac{1}{a_2},\frac{1}{a_4}$成等比数列.(1)求数列{an}的通项公式;
(2)对n∈N*,试比较$\frac{1}{a_2}+\frac{1}{a_4}+\frac{1}{a_8}+…+\frac{1}{{{a_{2^n}}}}$与$\frac{1}{a_1}$的大小.
分析 (1)设等差数列{an}的公差为d,由题意可知,$(\frac{1}{{a}_{2}})^{2}=\frac{1}{{a}_{1}}•\frac{1}{{a}_{4}}$
可得d=a1=a.即通项公式an=na.
(2)记Tn=$\frac{1}{a_2}+\frac{1}{a_4}+\frac{1}{a_8}+…+\frac{1}{{{a_{2^n}}}}$
Tn=$\frac{1}{a}$($\frac{1}{2}$+$\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$)=$\frac{1}{a}$•$\frac{\frac{1}{2}[1-\frac{1}{{2}^{n}}]}{1-\frac{1}{2}}$=$\frac{1}{a}$[1-($\frac{1}{2}$)n].
,当a>0时,Tn<$\frac{1}{{a}_{1}}$;当a<0时,Tn>$\frac{1}{{a}_{1}}$.
解答 解:(1)设等差数列{an}的公差为d,由题意可知,$(\frac{1}{{a}_{2}})^{2}=\frac{1}{{a}_{1}}•\frac{1}{{a}_{4}}$
即(a1+d)2=a1(a1+3d),从而a1d=d2,
因为d≠0,所以d=a1=a.故通项公式an=na.
(2)记Tn=$\frac{1}{a_2}+\frac{1}{a_4}+\frac{1}{a_8}+…+\frac{1}{{{a_{2^n}}}}$
因为a2n=2na,
所以Tn=$\frac{1}{a}$($\frac{1}{2}$+$\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$)
=$\frac{1}{a}$•$\frac{\frac{1}{2}[1-\frac{1}{{2}^{n}}]}{1-\frac{1}{2}}$=$\frac{1}{a}$[1-($\frac{1}{2}$)n].
从而,当a>0时,Tn<$\frac{1}{{a}_{1}}$;
当a<0时,Tn>$\frac{1}{{a}_{1}}$.
点评 本题考查了等差、等比数列的性质,数列求和,考查了计算能力,属于中档题.

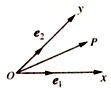 如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )
如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )| A. | $\overrightarrow{{e}_{1}}$=(1,0) | B. | |$\overrightarrow{OA}$|=2$\sqrt{3}$ | C. | $\overrightarrow{OA}$∥$\overrightarrow{BC}$ | D. | $\overrightarrow{OA}$⊥$\overrightarrow{OB}$ |
| A. | $\frac{\sqrt{5}}{2}$ | B. | 3 | C. | $\frac{\sqrt{10}}{2}$ | D. | 2 |
| A. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ | B. | $\frac{5}{4}$或5 | C. | 5 | D. | $\sqrt{5}$ |