题目内容
3．在斜三角形ABC中，tanA+tanB+tanAtanB=1，则∠C=135°．分析 由条件利用两角和的正切公式求得tan（A+B）=1，可得A+B的值，从而求得C的值．
解答 解：△ABC中，已知tanA+tanB+tanAtanB=1，
∴tan（A+B）（1-tanAtanB）+tanAtanB=1，
∴tan（A+B）（1-tanAtanB）=1-tanAtanB，
∴tan（A+B）=1，
∴A+B=45°，
∴C=135°．
故答案为：135°．
点评 本题主要考查两角和的正切公式在三角函数化简求值中的应用，考查了转化思想，属于基础题．
练习册系列答案
相关题目
有一块半径为R（R为正常数）的半圆形空地，开发商计划征地建一个游泳池ABCD和其附属设施，附属设施占地形状是等腰△CDE，其中O为圆心，A，B在圆的直径上，C，D，E在半圆周上，如图．
15．
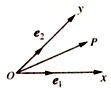如图，设Ox、Oy是平面内相交成45°角的两条数轴，$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量，若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$，则把有序数对（x，y）叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标，在此坐标系下，假设$\overrightarrow{OA}$=（-2，2$\sqrt{2}$），$\overrightarrow{OB}$=（2，0），$\overrightarrow{OC}$=（5，-3$\sqrt{2}$），则下列命题不正确的是（ ）
如图，设Ox、Oy是平面内相交成45°角的两条数轴，$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量，若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$，则把有序数对（x，y）叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标，在此坐标系下，假设$\overrightarrow{OA}$=（-2，2$\sqrt{2}$），$\overrightarrow{OB}$=（2，0），$\overrightarrow{OC}$=（5，-3$\sqrt{2}$），则下列命题不正确的是（ ）| A． | $\overrightarrow{{e}_{1}}$=（1，0） | B． | |$\overrightarrow{OA}$|=2$\sqrt{3}$ | C． | $\overrightarrow{OA}$∥$\overrightarrow{BC}$ | D． | $\overrightarrow{OA}$⊥$\overrightarrow{OB}$ |
10．已知圆M：（x-2a）2+y2=4a2与双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）交于A、B两点，点D为圆M与x轴正半轴的交点，点E为双曲线C的左顶点，若四边形EADB为菱形，则双曲线C的离心率为（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | 3 | C． | $\frac{\sqrt{10}}{2}$ | D． | 2 |