题目内容
18.如果将直线l:x+2y+c=0向左平移1个单位,再向下平移2个单位,所得直线l′与圆C:x2+y2+2x-4y=0相切,则实数c的值构成的集合为{-3,-13}.分析 由图象平移可得直线l′的方程,化圆的方程为标准方程可得圆心和半径,由点到直线的距离公式可得c的方程,解方程可得.
解答 解:直线l:x+2y+c=0可化为y=-$\frac{1}{2}$x-$\frac{1}{2}$c,
向左平移1个单位得到y=-$\frac{1}{2}$(x+1)-$\frac{1}{2}$c,
再向下平移2个单位得到y=-$\frac{1}{2}$(x+1)-$\frac{1}{2}$c-2,
整理可得直线l′的方程为x+2y+c+5=0,
又圆C:x2+y2+2x-4y=0可化为(x+1)2+(y-2)2=5,
故圆心为(-1,2),半径为$\sqrt{5}$
由直线和相切可得$\frac{|-1+2×2+c+5|}{\sqrt{{1}^{2}+{2}^{2}}}$=$\sqrt{5}$,
解方程可得c=-3或c=-13
故答案为:{-3,-13}
点评 本题考查直线和圆的位置关系,涉及图象平移和点到直线的距离公式,属中档题.

练习册系列答案
相关题目
14.如果ξ是1个离散型随机变量,那么下列命题中假命题是( )
| A. | ξ取每个可能值的概率是非负数 | |
| B. | ξ取所有可能值的概率之和为1 | |
| C. | ξ取某2个可能值的概率等于分别取其中这2个值的概率之和 | |
| D. | ξ的取值只能是正整数 |
13.已知点P(1,$\sqrt{5}$)在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线上,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
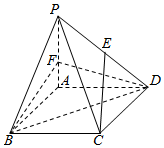 如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°,PA⊥面ABCD,且PA=3.E为PD中点,F在棱PA上,且AF=1
如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°,PA⊥面ABCD,且PA=3.E为PD中点,F在棱PA上,且AF=1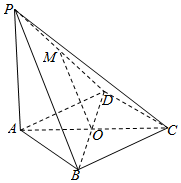 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.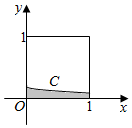 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(-2,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(-2,1)的密度曲线)的点的个数的估计值为( )