题目内容
15.若方程为$\frac{x^2}{m+1}-\frac{y^2}{m-3}$=1表示双曲线,则实数m满足( )| A. | m>3或m<-1 | B. | m≠-1且m≠3 | C. | -1<m<3 | D. | m<-1 |
分析 利用双曲线的简单性质,列出不等式求解即可.
解答 解:方程为$\frac{x^2}{m+1}-\frac{y^2}{m-3}$=1表示双曲线,
可得(m+1)(m-3)>0,解得m>3或m<-1.
故选:A.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.一块边长为6cm的正方形铁皮按如图(1)所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正三棱锥形容器,将该容器按如图(2)放置,若其正视图为等腰直角三角形(如图(3)),则该容器的体积为( )
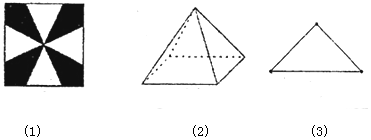

| A. | $12\sqrt{6}c{m^3}$ | B. | $4\sqrt{6}c{m^3}$ | C. | $27\sqrt{2}c{m^3}$ | D. | $9\sqrt{2}c{m^3}$ |
20.设M={x|x=a2+1,a∈R},P={y|y=b2-4b+5,b∈R},则下列关系正确的是( )
| A. | M=P | B. | M?P | ||
| C. | P?M | D. | M与P没有公共元素 |
5.已知点A(-5,0),B(5,0),直线AM,BM的交点为M,AM,BM的斜率之积为$-\frac{16}{25}$,则点M的轨迹方程是( )
| A. | $\frac{x^2}{25}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | ||
| C. | $\frac{x^2}{25}-\frac{y^2}{16}=1({x≠±5})$ | D. | $\frac{x^2}{25}+\frac{y^2}{16}=1({x≠±5})$ |