题目内容
函数f（x）=xln（ax）（a＜0）的递增区间是 ．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求单调区间先求定义域，再根据f'（x）＞0解出x的范围即可．
解答：
解：∵a＜0，∴定义域为（-∞，0），f'（x）=ln（ax）+1，当f'（x）＞0时，函数f（x）递增，此时ax＞
∴x＜
＜0，故递增区间为(-∞，
)．
故答案为：(-∞，
)
| 1 |
| e |
| 1 |
| ae |
| 1 |
| ae |
故答案为：(-∞，
| 1 |
| ae |
点评：本题考查函数的导数的应用，函数的单调区间的求法，考查分析问题解决问题的能力．
练习册系列答案
相关题目
已知x＞0，y＞0，且x+y+xy=2，则xy的最大值为（ ）
A、1+
| ||
B、
| ||
C、4-2
| ||
D、4+2
|
设M={3，5，6，8}，N={4，5，7，8}，则M∩N=（ ）
| A、{3，4，5，6，7，8} |
| B、{3，6} |
| C、{5，8} |
| D、{5，6，7，8} |
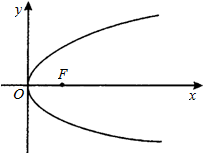已知抛物线C的顶点在原点，焦点F在x轴上，抛物线上的点A到F的距离为2，且A的横坐标为1．