题目内容
14.已知数列{an}满足${a_n}+{a_{n+1}}=\frac{1}{2}({n∈{N^*}})$,其前n项和为Sn,a2=2,则S21=( )| A. | 5 | B. | $\frac{7}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{13}{2}$ |
分析 ${a_n}+{a_{n+1}}=\frac{1}{2}({n∈{N^*}})$,a2=2,可得a1+2=$\frac{1}{2}$,解得a1.a2n+a2n+1=$\frac{1}{2}$,即可得出.
解答 解:∵${a_n}+{a_{n+1}}=\frac{1}{2}({n∈{N^*}})$,a2=2,∴a1+2=$\frac{1}{2}$,解得a1=-$\frac{3}{2}$.
∴a2n+a2n+1=$\frac{1}{2}$,
∴S21=-$\frac{3}{2}$+$\frac{1}{2}×$10=$\frac{7}{2}$.
故选:B.
点评 本题考查了数列递推关系、分组求和方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.设M{a,b,c}=$\left\{\begin{array}{l}{a,b,c的中位数,(a-b)(b-c)(c-a)≠0}\\{a,b,c的众数,(a-b)(b-c)(c-a)=0}\end{array}\right.$,若f(x)=M{2x,x2,4-7.5x}(x>0),则f(x)的最小值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{4}$ |
5.某兴趣小组在网上看见一则消息称哈尔滨工业大学男女比例近似满足4:1,由于哈工大的专业偏向理科,该小组猜想高中生的文理科选修与性别有关.为了判断高中生的文理科选修是否与性别有关,该小组随机调查了100名学生的情况,得到如下图所示的2×2列联表
(1)请补全该2×2列联表.
(2)试通过计算说明,能否有99%的把握认为高中生的文理科选修是与性别有关.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)},其中n=({a+b+c+d})$
| 理科 | 文科 | 合计 | |
| 男 | 30 | ||
| 女 | 35 | 45 | |
| 合计 | 60 |
(2)试通过计算说明,能否有99%的把握认为高中生的文理科选修是与性别有关.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)},其中n=({a+b+c+d})$
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| K0 | 0.445 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
2.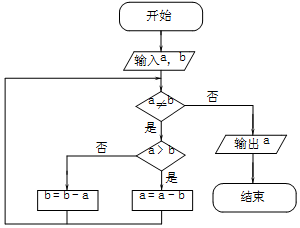 更相减损术是出自中国古代数学专著《九章算术》的一种算法,其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.”右图是该算法的程序框图,如果输入a=153,b=119,则输出的a值是( )
更相减损术是出自中国古代数学专著《九章算术》的一种算法,其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.”右图是该算法的程序框图,如果输入a=153,b=119,则输出的a值是( )
 更相减损术是出自中国古代数学专著《九章算术》的一种算法,其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.”右图是该算法的程序框图,如果输入a=153,b=119,则输出的a值是( )
更相减损术是出自中国古代数学专著《九章算术》的一种算法,其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.”右图是该算法的程序框图,如果输入a=153,b=119,则输出的a值是( )| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
9.已知a,b,c满足a>b>c,ac<0,则下列不等关系中正确的是( )
| A. | cb2<ab2 | B. | ab<ac | C. | c(a-c)>0 | D. | a+ac>b+ac |
6.下列哪个函数是周期为π的偶函数( )
| A. | y=sin2x | B. | y=|sin2x| | C. | y=cos2x | D. | y=|cos2x| |
3.已知集合A={1,2},B={x|x=a+b,a∈A,b∈A},则集合B中元素个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |