题目内容
4.设M{a,b,c}=$\left\{\begin{array}{l}{a,b,c的中位数,(a-b)(b-c)(c-a)≠0}\\{a,b,c的众数,(a-b)(b-c)(c-a)=0}\end{array}\right.$,若f(x)=M{2x,x2,4-7.5x}(x>0),则f(x)的最小值是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{4}$ |
分析 对分段函数分类讨论,当(2x-x2)(x2-4+7.5x}(4-7.5x-2x)=0时,f(x)=2x,x2,4-7.5x众数,分别求解,得出f(x)的最小值是;
做出函数y=2x,y=x2,y=4-7.5x的图象,利用数学结合得出当(2x-x2)(x2-4+7.5x}(4-7.5x-2x)≠0时,f(x)=2x,x2,4-7.5x的中位数范围.
解答 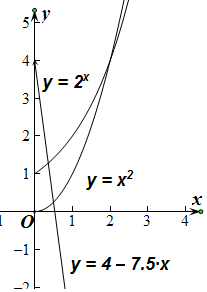 解:由题意,f(x)=M{2x,x2,4-7.5x},
解:由题意,f(x)=M{2x,x2,4-7.5x},
当(2x-x2)(x2-4+7.5x}(4-7.5x-2x)≠0时,
f(x)=2x,x2,4-7.5x的中位数,
当(2x-x2)(x2-4+7.5x}(4-7.5x-2x)=0时,
f(x)=2x,x2,4-7.5x众数,
令(2x-x2)(x2-4+7.5x)(4-7.5x-2x)=0,
若2x=x2,则x=2或4,
若x2=4-7.5x,则x=-8(舍去)或$\frac{1}{2}$,
若2x=4-7.5x,
令g(x)=2x-4+7.5x,
∵g(0)=1-4+0=-3<0,g($\frac{1}{2}$)=$\sqrt{2}$-4+3.75>0,
∴x∈(0,$\frac{1}{2}$);
∴(2x-x2)(x2-4+7.5x}(4-7.5x-2x)=0时,f(x)=$\frac{1}{4}$
当(2x-x2)(x2-4+7.5x}(4-7.5x-2x)≠0时,f(x)=2x,x2,4-7.5x的中位数,
由右侧图象可知:中位数都大于$\frac{1}{4}$,
故选A.
点评 本题考查了新定义函数和分段函数的处理.难点是利用数学结合解决实际问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.茎叶图如图1,为高三某班60名学生的化学考试成绩,算法框图如图2中输入的a1为茎叶图中的学生成绩,则输出的m,n分别是( )
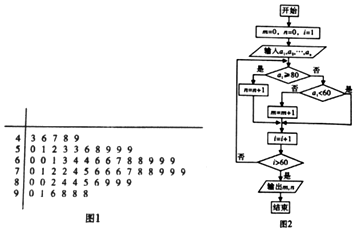

| A. | m=29,n=15 | B. | m=29,n=16 | C. | m=15,n=16 | D. | m=16,n=15 |
12.已知函数f(x)=x4cosx+mx2+2x(m∈R),若导函数f'(x)在区间[-4,4]上有最大值16,则导函数f'(x)在区间[-4,4]上的最小值为( )
| A. | -16 | B. | -12 | C. | 12 | D. | 16 |
14.已知数列{an}满足${a_n}+{a_{n+1}}=\frac{1}{2}({n∈{N^*}})$,其前n项和为Sn,a2=2,则S21=( )
| A. | 5 | B. | $\frac{7}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{13}{2}$ |