题目内容

2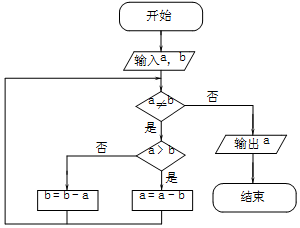．更相减损术是出自中国古代数学专著《九章算术》的一种算法，其内容如下：“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也．以等数约之．”右图是该算法的程序框图，如果输入a=153，b=119，则输出的a值是（　　）
A．16B．17C．18D．19

分析 由循环结构的特点，先判断，再执行，分别计算出当前的a，b的值，即可得到结论．

解答 解：第一次循环得：a=153-119=34；
第二次循环得：b=119-34=85；
第三次循环得：b=85-34=51；
同理，第四次循环b=51-34=17；
第五次循环a=34-17=17，
此时a=b，输出a=17，
故选：B．

点评 本题考查算法和程序框图，主要考查循环结构的理解和运用，以及赋值语句的运用，属于基础题．

练习册系列答案
相关题目
12．已知函数f（x）=x4cosx+mx2+2x（m∈R），若导函数f'（x）在区间[-4，4]上有最大值16，则导函数f'（x）在区间[-4，4]上的最小值为（　　）
A．-16B．-12C．12D．16
13．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1、F2，离心率为$\frac{\sqrt{3}}{3}$，点M在椭圆上，且满足MF2⊥x轴，|MF1|=$\frac{4\sqrt{3}}{3}$．
（1）求椭圆的方程；
（2）过F1，F2分别作互相垂直的两直线与椭圆C分别交于D、E、M、N四点，试求四边形DMEN面积的最大值和最小值．
10．已知直线l1：ax-y-1=0，若直线l1的倾斜角为$\frac{π}{3}$，则a=$\sqrt{3}$．
17．已知二项式（x-$\frac{a}{\root{3}{x}}$）4的展开式中常数项为32，则a=（　　）
A．8B．-8C．2D．-2
7．已知g（x）=mx，G（x）=lnx．
（Ⅰ）若G（x）+x+2≤g（x）恒成立，求m的取值范围；
（Ⅱ）令b=G（a）+a+2，求证：b-2a≤1．
14．已知数列{an}满足${a_n}+{a_{n+1}}=\frac{1}{2}（{n∈{N^*}}）$，其前n项和为Sn，a2=2，则S21=（　　）
A．5B．$\frac{7}{2}$C．$\frac{9}{2}$D．$\frac{13}{2}$
11．$f（x）=\sqrt{3}sinx-cosx$，求：
（1）求周期、振幅；
（2）求[0，π]在区间[0，π]上的值域．
12．已知函数f（x）=$\left\{\begin{array}{l}{a•{2}^{x}，x≤0}\\{lo{g}_{2}x，x＞0}\end{array}\right.$，若关于x的方程f（f（x））=0有且只有一个实数解，则实数a的取值范围是（　　）
A．（-∞，0）B．（-∞，0]∪（0，1）C．（-∞，0）∪（0，1]D．（-∞，0）∪（0，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网