题目内容

当x∈[1，5]时，函数f（x）=3x2-4x+c的值域为（　　）
A、[f（1），f（5）]
B、[f（1），f（
2
3
）]
C、[f（
2
3
），f（5）]
D、[c，f（5）]
考点：二次函数在闭区间上的最值,二次函数的性质
专题：函数的性质及应用
分析：确定对称轴x=
2
3
，根据[1，5]单调递增，求解即可．
解答： 解：∵函数f（x）=3x2-4x+c，对称轴x=
2
3
，
∴x∈[1，5]单调递增，
∴f（x）的值域为[f（1），f（5）]、
故选：A
点评：本题考查了二次函数的性质，关键是确定对称轴，与区间的关系，属于容易题．
练习册系列答案
相关题目
试将以下各式化为Asin（α+β）（A＞0，β∈[-π，π））的形式．
（1）sinα+cosα；
（2）cosα-sinα；
（3）3sinα-4cosα．
已知函数f（x）=mxlnx（m＞0），f（x）在点（e，f（e））处的切线与x轴、y轴分别交于A、B两点，且△AOB的面积为
e2
4
，证明：当x＞e时，对于任意正实数t不等式f（x+t）＜f（x）et恒成立．
若对于任何实数，二次不等式ax2-x+c＜0的解集为R，那么a、c应满足（　　）
A、a＞0且ac≤
1
4
B、a＜0且ac＜
1
4
C、a＜0且ac＞
1
4
D、a＜0且ac＜0
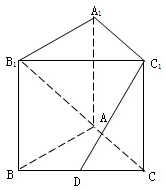如图，在三棱柱ABC-A1B1C1中，侧棱与底面垂直，已知AB=AC=AA1=2，
∠BAC=90°，若D为BC的中点，则AB1与C1D所成角的余弦值为
 
．
已知
1
3
≤a≤1，若函数f（x）=ax2-2x在[1，3]上的最大值为M（a），最小值为N（a），令g（a）=M（a）-N（a）．
（1）求g（a）的表达式；
（2）若关于a的方程g（a）-t=0有解，求实数t的取值范围．
求y=sin（2x+
π
3
）在[-
π
2
，
π
4
]的最值．
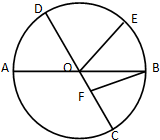如图所示，在⊙O中，AB与CD是夹角为60°的两条直径，E、F分别是⊙O与直径CD上的动点，若
OE
•
BF
+λ
OA
•
OC
=0，则λ的取值范围是
 
．
在△ABC中，角A、B、C所对的边分别为a，b，c，且cosA=
1
3
，则sin2
B+C
2
+cos2A的值为（　　）
A、
1
9
B、-
1
9
C、
1
10
D、-
1
10

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网