题目内容
4.给出以下命题:①方程4x2-8x+3=0的两个根可分别作为椭圆与双曲线的离心率;
②若向量$\overrightarrow{a}$=(m,-2,3)与$\overrightarrow{b}$=(5,m2,1)的夹角为锐角,则-$\frac{1}{2}$<m<3;
③在正项等差数列{an}中,$\frac{a_3}{a_2+a_9}$+$\frac{a_8}{a_5+a_6}$=1;
④当x>0时,函数f(x)=x2+$\frac{1}{x^2}$-8x-$\frac{8}{x}$+22的最小值是4.
其中正确命题的序号是①②③④.
分析 ①求出方程的根,结合椭圆和双曲线离心率的关系进行判断.
②根据向量数量积的应用进行求解.
③根据等差数列的性质进行求解.
④利用换元法结合基本不等式以及一元二次函数的性质进行求解.
解答 解:①由4x2-8x+3=0得x=$\frac{1}{2}$或x=$\frac{3}{2}$,即方程的两个根可分别作为椭圆与双曲线的离心率;故①正确,
②若向量$\overrightarrow{a}$=(m,-2,3)与$\overrightarrow{b}$=(5,m2,1)的夹角为锐角,则$\overrightarrow{a}•\overrightarrow{b}$>0,(∵两个向量方向不相同),
∴5m-2m2+3>0,即2m2-5m-3<0,得-$\frac{1}{2}$<m<3;故②正确,
③在正项等差数列{an}中,$\frac{a_3}{a_2+a_9}$+$\frac{a_8}{a_5+a_6}$=$\frac{{a}_{3}+{a}_{8}}{{a}_{2}+{a}_{9}}=\frac{{a}_{2}+{a}_{9}}{{a}_{2}+{a}_{9}}$=1,故③正确;
④当x>0时,函数f(x)=x2+$\frac{1}{x^2}$-8x-$\frac{8}{x}$+22=(x+$\frac{1}{x}$)2-8(x+$\frac{1}{x}$)+20,
设t=x+$\frac{1}{x}$,则t≥2,此时函数等价为y=t2-8t+20=(t-4)2+4,
故当t=4时,函数取得的最小值4,故④正确,
故答案为:①②③④
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不大.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
15.圆x2+y2=4与圆x2+y2-4y+3=0的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
19.已知集合A={x|x2<1},集合B={x|$\frac{1}{x}$<1},则A∩B=( )
| A. | (-1,0) | B. | (0,1) | C. | (1,+∞) | D. | ∅ |
16.用反证法证明某命题时,对其结论:“自然数a,b,c中恰有一个偶数”正确的反设为( )
| A. | a,b,c都是奇数 | |
| B. | a,b,c中至少有两个偶数或都是奇数 | |
| C. | a,b,c中至少有两个偶数 | |
| D. | a,b,c都是偶数 |
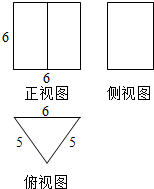 某几何体的三视图如图所示,其中正视图是边长为6的正方形,俯视图是腰长为5,底边长为6的等腰三角形,则该几何体的体积是72,表面积是120.
某几何体的三视图如图所示,其中正视图是边长为6的正方形,俯视图是腰长为5,底边长为6的等腰三角形,则该几何体的体积是72,表面积是120. 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测的公路北侧一山顶D在西偏北30°的方向上,行驶1200m后到达B处,测得此山顶D在西偏北75°的方向上,仰角为60°,则此山的高度CD=600$\sqrt{6}$m.
如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测的公路北侧一山顶D在西偏北30°的方向上,行驶1200m后到达B处,测得此山顶D在西偏北75°的方向上,仰角为60°,则此山的高度CD=600$\sqrt{6}$m.