题目内容
6.在数列{an}中,a1=$\frac{1}{2}$,an+1=$\frac{3{a}_{n}}{{a}_{n}+3}$,求a2、a3、a4的值,由此猜想数列{an}的通项公式,并证明你的猜想.分析 求出数列的前几项,猜想通项公式,然后利用数学归纳法证明步骤证明即可.
解答 解:a1=$\frac{1}{2}$=$\frac{3}{6}$,a2=$\frac{3}{7}$,a3=$\frac{3}{8}$,a4=$\frac{3}{9}$,
猜想an=$\frac{3}{n+5}$,下面用数学归纳法证明:
①当n=1时,a1=$\frac{3}{1+5}$=$\frac{1}{2}$,猜想成立.
②假设当n=k(k≥1,k∈N*)时猜想成立,
即ak=$\frac{3}{k+5}$.则当n=k+1时,
ak+1=$\frac{3{a}_{k}}{{a}_{k}+3}$=$\frac{3•\frac{3}{k+5}}{\frac{3}{k+5}+3}$=$\frac{3}{(k+1)+5}$,
所以当n=k+1时猜想也成立,
由①②知,对n∈N*,an=$\frac{3}{n+5}$都成立
点评 本题考查数学归纳法法应用,考查逻辑推理能力以及计算能力.

练习册系列答案
相关题目
20.集合A={x|x2-4=0}的子集个数( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
1.一个几何体的三视图如图所示,则该几何体的表面积为( )
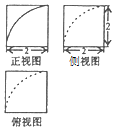

| A. | 24+π | B. | 24-3π | C. | 24-π | D. | 24-2π |
14.某校高二2班学生每周用于数学学习的时间x(单位:h)与数学成绩y(单位:分)之间有如表数据:
(Ⅰ)求线性回归方程;
(Ⅱ)该班某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
参考数据:$\overline x=17.4$,$\overline y=74.9$,$\sum_{i=1}^{10}{{x_i}^2=3182}$,$\sum_{i=1}^{10}{{y_i}^2=58375}$,$\sum_{i=1}^{10}{{x_i}{y_i}=13578}$
回归直线方程参考公式:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
(Ⅱ)该班某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
参考数据:$\overline x=17.4$,$\overline y=74.9$,$\sum_{i=1}^{10}{{x_i}^2=3182}$,$\sum_{i=1}^{10}{{y_i}^2=58375}$,$\sum_{i=1}^{10}{{x_i}{y_i}=13578}$
回归直线方程参考公式:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.