题目内容
9. 对某电子元件进行寿命追踪调查,情况如表.
对某电子元件进行寿命追踪调查,情况如表.| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个 数 | 20 | 30 | 80 | 40 | 30 |
(2)从频率分布直方图估计出电子元件寿命的众数、中位数分别是多少?
分析 (1)根据题意,列出样本频率分布表、画出频率分布直方图即可;
(2)根据频率分布直方图,计算众数与中位数的值.
解答 解:(1)根据题意,列出样本频率分布表如下;
| 寿命(h) | 频 数 | 频 率 |
| 100~200 | 20 | 0.10 |
| 200~300 | 30 | 0.15 |
| 300~400 | 80 | 0.40 |
| 400~500 | 40 | 0.20 |
| 500~600 | 30 | 0.15 |
| 合 计 | 200 | 1.00 |
画出频率分布直方图,如下;
 --(9分)
--(9分)(2)从频率分布直方图可以看出电子元件寿命的众数是$\frac{300+400}{2}$=350;--(10分)
中位数为:$200+\frac{0.5-0.001×100-0.0015×100}{0.004}=200+\frac{0.25}{0.0004}=262.5$.-(12分)
点评 本题考查了频率分布直方图的应用问题,是基础题目.

练习册系列答案
相关题目
17.在△ABC中,角A,B,C所对的边分别为a,b,c,那么a>b是sinA>sinB的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | C. | 充分且必要 | D. | 无关 |
4.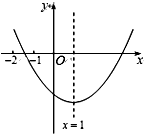 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
①b2-4ac>0;
②abc>0;
③b=-2a;
④9a+3b+c<0,
正确结论的个数是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:①b2-4ac>0;
②abc>0;
③b=-2a;
④9a+3b+c<0,
正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.若集合M={y|y=3x},N={x|y=$\sqrt{1-3x}$},则M∩N=( )
| A. | [0,$\frac{1}{3}$] | B. | (0,$\frac{1}{3}$] | C. | (0,+∞) | D. | (-∞,$\frac{1}{3}$] |
1.为了得到函数y=sin2x-cos2x的图象,可以将函数y=$\sqrt{2}$cos2x的图象( )
| A. | 向左平行移动$\frac{3π}{8}$个单位 | B. | 向右平行移动$\frac{3π}{8}$个单位 | ||
| C. | 向左平行移动$\frac{3π}{4}$个单位 | D. | 向右平行移动$\frac{3π}{4}$个单位 |
 某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如图(部分有缺损):
某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如图(部分有缺损):