题目内容
19. 某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如图(部分有缺损):
某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如图(部分有缺损):(1)补全频率分布直方图(需写出计算过程);
(2)现从[40,55)岁年龄段样本中采用分层抽样方法抽取6人分成A、B两个小组(每组3人)参加户外体验活动,记A组中年龄在[40,45)岁的人数为ξ,
求随机变量ξ的分布列和数学期望Eξ.
分析 (1)第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5,作出频率直方图,如右图.
(2)由[40,45)组,[45,50)组和[50,55)组的人数比为0.03:0.02:0.01=3:2:1,
因此三组中抽出的人数分别为3,2,1,ξ=0,1,2,3,利用P(ξ=i)=$\frac{{∁}_{3}^{i}{∁}_{3}^{3-i}}{{∁}_{6}^{3}}$(i=0,1,2,3)即可得出.
解答 解:(1)∵第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,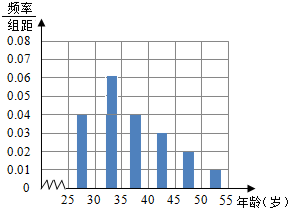
∴高为0.3÷5=0.06.
作出频率直方图,如右图.
(2)∵[40,45)组,[45,50)组和[50,55)组的人数比为0.03:0.02:0.01=3:2:1,
∴三组中抽出的人数分别为3,2,1,
ξ=0,1,2,3,
P(ξ=0)=$\frac{{∁}_{3}^{0}}{{∁}_{6}^{3}}$=$\frac{1}{20}$,P(ξ=1)=$\frac{{∁}_{3}^{1}{∁}_{3}^{2}}{{∁}_{6}^{3}}$=$\frac{9}{20}$,
P(ξ=2)=$\frac{{∁}_{3}^{2}{∁}_{3}^{1}}{{∁}_{6}^{3}}$=$\frac{9}{20}$,P(ξ=3)=$\frac{{∁}_{3}^{3}}{{∁}_{6}^{3}}$=$\frac{1}{20}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{20}$ | $\frac{9}{20}$ | $\frac{9}{20}$ | $\frac{1}{20}$ |
点评 本题考查了频率分布直方图、超几何的分布列的概率计算与数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.设l是直线,α和β是平面,则下列说法正确的是( )
| A. | 若α⊥β,l∥α,则l⊥β | B. | 若α⊥β,l⊥a,则l∥β | C. | 若l∥α,l∥β,则α∥β | D. | 若l∥α,l⊥β,则α⊥β |
4.设函数f(x)=$\left\{\begin{array}{l}x^2,x≥0\\ ln(-x),x<0\end{array}$,则函数g(x)=f(x)-x的零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9. 对某电子元件进行寿命追踪调查,情况如表.
对某电子元件进行寿命追踪调查,情况如表.
(1)列出频率分布表,并画出频率分布直方图;
(2)从频率分布直方图估计出电子元件寿命的众数、中位数分别是多少?
 对某电子元件进行寿命追踪调查,情况如表.
对某电子元件进行寿命追踪调查,情况如表.| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个 数 | 20 | 30 | 80 | 40 | 30 |
(2)从频率分布直方图估计出电子元件寿命的众数、中位数分别是多少?