Question

3．如图，在正方体ABCD-A₁B₁C₁D₁中，点E₁、F₁分别是A₁B₁、C₁D₁的四等分点，求BE₁与DF₁所成角的余弦值．

Answer 1

分析 以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，利用向量法能求出BE₁与DF₁所成角的余弦值．

解答 解：以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，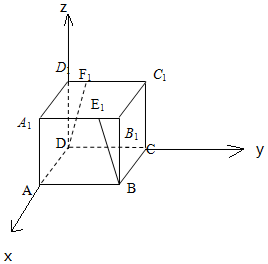
设正方体ABCD-A₁B₁C₁D₁中棱长为4，
则B（4，4，0），E₁（4，3，4），D（0，0，0），
F₁（0，1，4），
$\overrightarrow{B{E}_{1}}$=（0，-1，4），$\overrightarrow{D{F}_{1}}$=（0，1，4），
设BE₁与DF₁所成角为θ，
则cosθ=$\frac{|\overrightarrow{B{E}_{1}}•\overrightarrow{D{F}_{1}}|}{|\overrightarrow{B{E}_{1}}|•|\overrightarrow{D{F}_{1}}|}$=$\frac{15}{\sqrt{17}•\sqrt{17}}$=$\frac{15}{17}$．
∴BE₁与DF₁所成角的余弦值为$\frac{15}{17}$．

点评 本题考查异面直线所成角的余弦值的求法，是基础题，解题时要认真审题，注意向量法的合理运用．