题目内容
已知x>0,y>0,且x+8y-xy=0.求:
(Ⅰ)xy的最小值;
(Ⅱ)x+y的最小值.
(Ⅰ)xy的最小值;
(Ⅱ)x+y的最小值.
考点:基本不等式
专题:不等式的解法及应用
分析:(I)由x>0,y>0,且x+8y-xy=0,利用基本不等式可得xy=x+8y≥2
;
(II)由x>0,y>0,且x+8y-xy=0.变形为
+
=1,利用“乘1法”和基本不等式即可得出.
| 8xy |
(II)由x>0,y>0,且x+8y-xy=0.变形为
| 1 |
| y |
| 8 |
| x |
解答:
解:(I)∵x>0,y>0,且x+8y-xy=0,
∴xy=x+8y≥2
,化为xy≥32,当且仅当x=8y=16时取等号.
∴xy的最小值为32;
(II)∵x>0,y>0,且x+8y-xy=0.
∴
+
=1,
∴x+y=(x+y)(
+
)=9+
+
≥9+2
=9+4
,当且仅当x=2
y=2
+8时取等号.
故x+y的最小值为9+4
,
∴xy=x+8y≥2
| 8xy |
∴xy的最小值为32;
(II)∵x>0,y>0,且x+8y-xy=0.
∴
| 1 |
| y |
| 8 |
| x |
∴x+y=(x+y)(
| 1 |
| y |
| 8 |
| x |
| x |
| y |
| 8y |
| x |
|
| 2 |
| 2 |
| 2 |
故x+y的最小值为9+4
| 2 |
点评:本题考查了基本不等式的应用,利用基本不等式的性质,属于基础题.

练习册系列答案
相关题目
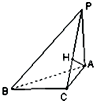 如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值.
如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值.