题目内容
△ABC中,∠C=90°,M是BC的中点,若sin∠BAM=
,则sin∠BAC=( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:解三角形
专题:综合题,解三角形
分析:作出图象,设出未知量,在△ABM中,由正弦定理可得sin∠AMB=
,进而可得cosβ=
,在RT△ACM中,还可得cosβ=
,建立等式后可得a=
b,再由勾股定理可得c=
b,即可得出结论.
| 2c |
| 3a |
| 2c |
| 3a |
| b | ||||
|
| 2 |
| 3 |
解答:
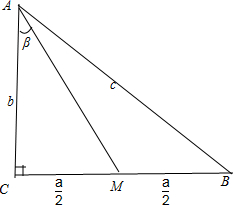 解:如图,设AC=b,AB=c,CM=MB=
解:如图,设AC=b,AB=c,CM=MB=
,∠MAC=β,
在△ABM中,由正弦定理可得
=
,
代入数据解得sin∠AMB=
,
故cosβ=cos(
-∠AMC)=sin∠AMC=sin(π-∠AMB)
=sin∠AMB=
,
而在RT△ACM中,cosβ=
=
,
故可得
,化简可得a4-4a2b2+4b4=(a2-2b2)2=0,
解之可得a=
b,再由勾股定理可得a2+b2=c2,联立可得c=
b,
故在RT△ABC中,sin∠BAC=
=
,
故选:B.
 解:如图,设AC=b,AB=c,CM=MB=
解:如图,设AC=b,AB=c,CM=MB=| a |
| 2 |
在△ABM中,由正弦定理可得
| ||
| sin∠BAM |
| c |
| sin∠AMB |
代入数据解得sin∠AMB=
| 2c |
| 3a |
故cosβ=cos(
| π |
| 2 |
=sin∠AMB=
| 2c |
| 3a |
而在RT△ACM中,cosβ=
| AC |
| AM |
| b | ||||
|
故可得
| b | ||||
|
| 2c |
| 3a |
解之可得a=
| 2 |
| 3 |
故在RT△ABC中,sin∠BAC=
| BC |
| AB |
| ||
| 3 |
故选:B.
点评:本题考查正弦定理的应用,涉及三角函数的诱导公式以及勾股定理的应用,属中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).求直线被圆C截得的弦长最小时l的方程.( )
| A、x-2y-1=0 |
| B、2x-y-5=0 |
| C、2x+y-7=0 |
| D、x+2y-5=0 |
设函数f(x)=
+cosx的所有正的极小值点从小到大排成的数列为{xn},则x1=( )
| x |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设A={1,2},B={2,3,4},则A∩B=( )
| A、{2} |
| B、{1,2} |
| C、{1,3,4} |
| D、{1,2,3,4} |
 函数y=f(x)的定义域为(a,b),y=f′(x)的图象如图,则函数y=f(x)在开区间(a,b)内取得极小值的点有( )
函数y=f(x)的定义域为(a,b),y=f′(x)的图象如图,则函数y=f(x)在开区间(a,b)内取得极小值的点有( )| A、1个 | B、2个 | C、3个 | D、4个 |
已知球O的表面积为12π,一个正方体的各顶点都在该球面上,则这个正方体的体积为( )
A、3
| ||
B、6
| ||
| C、8 | ||
| D、24 |
函数f(x)=lnx-
,则|f(x)|的极值点的个数是( )
| x-1 |
| e-1 |
| A、0 | B、1 | C、2 | D、3 |