题目内容
18．椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的一个焦点为F，该椭圆上有一点A，满足△OAF是等边三角形（O为坐标原点），则椭圆的离心率是（ ）| A． | $\sqrt{3}-1$ | B． | $2-\sqrt{3}$ | C． | $\sqrt{2}-1$ | D． | $2-\sqrt{2}$ |
分析 根据题意，作出椭圆的图象，分析可得A的坐标，将A的坐标代入椭圆方程可得$\frac{{c}^{2}}{4{a}^{2}}$+$\frac{3{c}^{2}}{4{b}^{2}}$=1，①；结合椭圆的几何性质a2=b2+c2，②；联立两个式子，解可得c=（$\sqrt{3}$-1）a，由离心率公式计算可得答案．
解答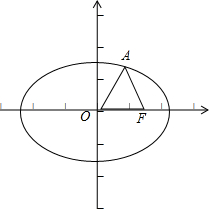 
解：根据题意，如图，设F（c，0），
又由△OAF是等边三角形，则A（$\frac{c}{2}$，$\frac{\sqrt{3}c}{2}$），
A在椭圆上，则有$\frac{{c}^{2}}{4{a}^{2}}$+$\frac{3{c}^{2}}{4{b}^{2}}$=1，①；
a2=b2+c2，②；
联立①②，解可得c=（$\sqrt{3}$-1）a，
则其离心率e=$\frac{c}{a}$=$\sqrt{3}$-1；
故选：A．
点评 本题考查椭圆的几何性质，关键是结合题意，由等边三角形的性质表示出A的坐标．
练习册系列答案
相关题目
8．设等差数列{an}的公差d≠0，a1=2d，若ak是a1与a2k+1的等比中项，则k=（ ）
| A． | 2 | B． | 3 | C． | 6 | D． | 8 |
9．已知sinα=$\frac{2}{3}$，则sin（2α-$\frac{π}{2}$）=（ ）
| A． | -$\frac{\sqrt{5}}{3}$ | B． | -$\frac{1}{9}$ | C． | $\frac{1}{9}$ | D． | $\frac{\sqrt{5}}{3}$ |
3．设α为钝角，且3sin2α=cosα，则sinα等于（ ）
| A． | $-\frac{1}{6}$ | B． | $\frac{1}{6}$ | C． | $\frac{{\sqrt{35}}}{6}$ | D． | $\frac{1}{3}$ |
7．
如图，在棱长为1的正方体ABCD-A1B1C1D1中，P，Q分别是线段CC1，BD上的点，R是直线AD上的点，满足PQ∥平面ABC1D1，PQ⊥RQ，且P、Q不是正方体的顶点，则|PR|的最小值是（ ）
如图，在棱长为1的正方体ABCD-A1B1C1D1中，P，Q分别是线段CC1，BD上的点，R是直线AD上的点，满足PQ∥平面ABC1D1，PQ⊥RQ，且P、Q不是正方体的顶点，则|PR|的最小值是（ ）| A． | $\frac{{\sqrt{42}}}{6}$ | B． | $\frac{{\sqrt{30}}}{5}$ | C． | $\frac{{\sqrt{5}}}{2}$ | D． | $\frac{{2\sqrt{3}}}{3}$ |