题目内容
13.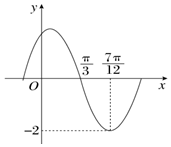 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,下列结论:
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,下列结论:①最小正周期为π;
②将f(x)的图象向左平移$\frac{π}{6}$个单位,所得到的函数是偶函数;
③f(0)=1;
④$f({\frac{12}{11}π})<f({\frac{14}{13}π})$.其中正确命题的序号是①④.
分析 由函数图象求出f(x)=2sin(2x+$\frac{π}{3}$),计算最小正周期T,判断①正确;
通过f(x)的图象向左平移$\frac{π}{6}$个单位,得y=2sin(2x+$\frac{2π}{3}$)的图象,判断②错误;
计算f(0)≠1,判断③错误;
求出x=$\frac{13π}{12}$是f(x)图象的一条对称轴,且在x=$\frac{13π}{12}$时f(x)取得最大值;
判断$f({\frac{12}{11}π})<f({\frac{14}{13}π})$,④正确.
解答 解:由函数图象可得:A=2,周期T=4($\frac{7π}{12}$-$\frac{π}{3}$)=π,∴①正确;
由周期公式可得:ω=$\frac{2π}{T}$=$\frac{2π}{π}$=2,
由点($\frac{π}{3}$,0)在函数的图象上,根据五点法画图得:
2sin(2×$\frac{π}{3}$+φ)=0,
解得$\frac{2π}{3}$+φ=π,得φ=$\frac{π}{3}$,
从而得f(x)=2sin(2x+$\frac{π}{3}$),
f(x)的图象向左平移$\frac{π}{6}$个单位,得y=2sin[2(x+$\frac{π}{6}$)+$\frac{π}{3}$]=2sin(2x+$\frac{2π}{3}$)的图象,
该函数不是偶函数,②错误;
f(0)=2sin$\frac{π}{3}$=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$≠1,∴③错误;
令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{3}$≤$\frac{π}{2}$+2kπ,k∈Z,
解得-$\frac{5π}{12}$+kπ≤x≤$\frac{π}{12}$+kπ,k∈Z;
当k=1时,得出f(x)在区间[$\frac{7π}{12}$,$\frac{13π}{12}$]上单调递增,在[$\frac{13π}{12}$,$\frac{19π}{12}$]上单调递减;
∴x=$\frac{13π}{12}$是f(x)图象的一条对称轴,且在x=$\frac{13π}{12}$时f(x)取得最大值;
又$\frac{π}{2}$>|$\frac{13π}{12}$-$\frac{12π}{11}$|>|$\frac{13π}{12}$-$\frac{14π}{13}$|,
∴$f({\frac{12}{11}π})<f({\frac{14}{13}π})$,∴④正确.
综上,正确命题的序号是①④.
故答案为:①④.
点评 本题考查了正弦型函数的图象与性质的应用问题,也考查了命题真假的判断问题,是综合性题目.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
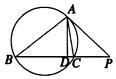 如图所示,PA切圆于A,PA=8,直线PCB交圆于C,B,连接AB,AC,且PC=4,AD⊥BC于D,∠ABC=α,∠ACB=β,则$\frac{sinα}{sinβ}$的值等于( )
如图所示,PA切圆于A,PA=8,直线PCB交圆于C,B,连接AB,AC,且PC=4,AD⊥BC于D,∠ABC=α,∠ACB=β,则$\frac{sinα}{sinβ}$的值等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
| A. | 2 | B. | 3 | C. | 6 | D. | 8 |
| 外语 | ||||
数学 | 优 | 良 | 及格 | |
| 优 | 8 | m | 9 | |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
(2)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
| A. | y=2x+2-x | B. | y=lg$\frac{1}{x+1}$ | C. | y=2|x| | D. | y=lg(x+$\sqrt{{x}^{2}+1}$) |
| A. | $-\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{{\sqrt{35}}}{6}$ | D. | $\frac{1}{3}$ |
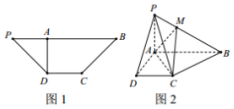 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB. 某几何体的三视图如图所不,则该几何体的表面积为22π+8.
某几何体的三视图如图所不,则该几何体的表面积为22π+8.