题目内容
6.设函数f(x)=$\frac{x^2}{{1+{x^2}}}$,利用课本中推导等差数列前n项和公式的方法,可求得f(1)+f(2)+f($\frac{1}{2}$)+f(3)+f($\frac{1}{3}$)+f(4)+f($\frac{1}{4}$)的值$\frac{7}{2}$.分析 行求出f(x)+f($\frac{1}{x}$)=1,由此能求出f(1)+f(2)+f($\frac{1}{2}$)+f(3)+f($\frac{1}{3}$)+f(4)+f($\frac{1}{4}$)的值.
解答 解:∵函数f(x)=$\frac{x^2}{{1+{x^2}}}$,
∴f(x)+f($\frac{1}{x}$)=$\frac{{x}^{2}}{1+{x}^{2}}$+$\frac{\frac{1}{{x}^{2}}}{1+\frac{1}{{x}^{2}}}$=$\frac{{x}^{2}}{1+{x}^{2}}+\frac{1}{{x}^{2}+1}$=1,
∴f(1)+f(2)+f($\frac{1}{2}$)+f(3)+f($\frac{1}{3}$)+f(4)+f($\frac{1}{4}$)
=f(1)+1+1+1
=$\frac{1}{1+1}+3$=$\frac{7}{2}$.
故答案为:$\frac{7}{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
16. 《九章算术》有如下问题:有上禾三秉(古代容量单位),中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗.问上、中、下禾一秉各几何?依上文:设上、中、下禾一秉分别为x斗、y斗、z斗,设计如图所示的程序框图,则输出的x,y,z的值分别为( )
《九章算术》有如下问题:有上禾三秉(古代容量单位),中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗.问上、中、下禾一秉各几何?依上文:设上、中、下禾一秉分别为x斗、y斗、z斗,设计如图所示的程序框图,则输出的x,y,z的值分别为( )
 《九章算术》有如下问题:有上禾三秉(古代容量单位),中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗.问上、中、下禾一秉各几何?依上文:设上、中、下禾一秉分别为x斗、y斗、z斗,设计如图所示的程序框图,则输出的x,y,z的值分别为( )
《九章算术》有如下问题:有上禾三秉(古代容量单位),中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗.问上、中、下禾一秉各几何?依上文:设上、中、下禾一秉分别为x斗、y斗、z斗,设计如图所示的程序框图,则输出的x,y,z的值分别为( )| A. | $\frac{37}{4},\frac{17}{4},\frac{11}{4}$ | B. | $\frac{11}{4},\frac{37}{4},\frac{17}{4}$ | C. | $\frac{35}{4},\frac{17}{4},\frac{9}{4}$ | D. | $\frac{35}{4},\frac{9}{4},\frac{17}{4}$ |
1.设点P对应的复数为1+i,以原点为极点,实轴正半轴为极轴建立极坐标系,则点P的极坐标为( )
| A. | ($\sqrt{2}$,$\frac{π}{4}$) | B. | ($-\sqrt{2}$,$\frac{3}{4}π$) | C. | (1,$\frac{3}{4}π$) | D. | (-1,$\frac{π}{4}$) |
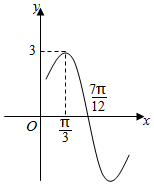 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).